Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.4 - Ex. 22
Em um circuito oscilante no qual , a diferença de potencial máxima entre os terminais do capacitor durante as oscilações é e a corrente máxima no indutor é . Determine (a) a indutância e (b) a frequência das oscilações. (c) Qual é o tempo necessário para que a carga do capacitor aumente de zero até o valor máximo?
Passo 1
Fala aí! tudo certinho? 😁
Aqui temos um circuito que a diferença de potencial máxima entre as placas do capacitor é e temos que a corrente máxima do indutor é . A partir daí temos que calcular a indutância , a frequência e o tempo necessário para a carga do capacitor.
Tem ideia de como fazemos isso? 😎
Para descobrir a indutância , podemos usar a relação
Sendo que .
Já para obter a frequência, usamos a equação
Saca só! 👀
Passo 2
(a) Usamos a relação para obter o valor de :
Como
Substituindo , e .
Tranquilo até aqui? 😉
Passo 3
(b)A frequência é dada por
Substituindo os valores de e ...
Bacana, né? 😁
Passo 4
(c) De acordo com a Fig. 31-1, o tempo necessário é um quarto do período.
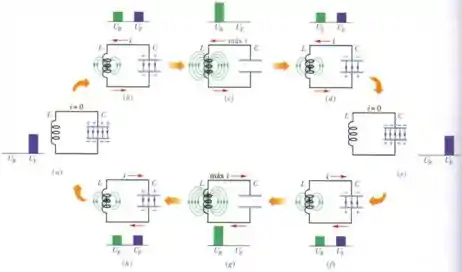
Assim,
Substituindo a frequência .
E aí! o que achou? Responde Aí! 😎
Resposta
(a)
(b)
(c)