Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 66
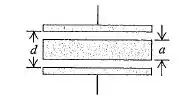
Um capacitor no ar possui placas largas, com área A, separadas por uma distância d. A seguir, uma placa metálica com espessura a (menor do que d), com as mesmas dimensões da área das placas, é inserida paralelamente entre as placas, sem tocar nenhuma delas. (Veja a figura abaixo) (a) Qual é a capacitância desse arranjo? (b) Expresse essa capacitância em função da capacitância existente antes da introdução da placa metálica. (c) Discuta o que ocorre com a capacitância nos limites e .
Passo 1
letra a)
No arranjo da figura, temos dois capacitores em série com uma separação entre as placas de , sendo que eles possuem a mesma capacitância.
Então:
Passo 2
Precisamos agora achar .
Podemos calcular a capacitância em termos da separação entre as placas:
Como a separação entre as placas a gente já sabe:
Passo 3
A capacitÂncia equivalente será:
Passo 4
letra b)
Antes da placa metálica a capacitância era:
Para expressar a nova capacitância em termos da antiga iremos fazer uma jogada!
Passo 5
letra c)
Para , logo
Para , logo
Resposta
letra a)
letra b)
letra c) , e ,