73- O campo elétrico de um fio retilíneo infinito com cargas positivas é direcionado radialmente para fora do fio e pode ser calculado a partir da Lei de Gauss para o campo elétrico (veja o Exemplo , na seção ). Aplique a lei de Gauss para o magnetismo para mostrar que o campo magnético de um condutor retilíneo infinito que conduz uma corrente não pode possuir um componente radial.

Cara basicamente o que essa questão quer é que com a seção transversal do fio, ao invés de encontrarmos o campo tangente a superfície ,que é a lei de Ampere e que fazemos pelo comprimento do círculo, temos que aplicar fazer a lei de Gauss e encontrar o valor do vetor magnético que está na área do círculo

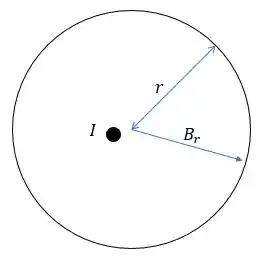
Então:

Isso nos diz que não existe nenhuma componente radial de campo magnético no fio.