Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 31.Exercícios e Problemas - Ex. 46

A Fig. 31-55 mostra uma seção transversal de um condutor cilíndrico, oco, de raios a e b, transportando uma corrente i uniformemente distribuída. (a) Mostre que B(r) para a faixa h

B = μ 0 i 2 π a 2 - b 2 r 2 - b 2 r

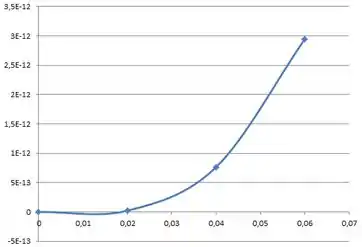
(b) Mostre que quando r = a esta equação dá o campo magnético B para um fio retilíneo longo; quando r = b dá campo magnético nulo e quando b = 0, dá o campo magnético no interior de um condutor sólido. (c) Suponha a = 2.0 cm, b= 1.8 cm e i = 100 A e taça o gráfico de B(r) na faixa 0

Passo 1

Fala galera, bora lá!

(a) A lei de Ampère é

∮ B   d s = μ 0 i

onde i é a corrente contida. Nosso loop Amperiano ainda será um círculo centrado no eixo do problema, então o lado esquerdo da equação acima será reduzido para 2 π r B . O lado direito, no entanto, depende da corrente líquida encerrada, que é a fração da corrente encerrada no condutor. A área da seção transversal do condutor é π ( a 2 - b 2 ) .

Passo 2

Então a fração da corrente encerrada no loop Amperiano é

i π r 2 - b 2 π a 2 - b 2 = i r 2 - b 2 a 2 - b 2

O campo magnético nesta região é

B = μ 0 i 2 π r   r 2 - b 2 a 2 - b 2

Passo 3

(b) Se r = a , então

B = μ 0 i 2 π a   a 2 - b 2 a 2 - b 2 = μ 0 i 2 π a

que é o que esperamos.

Passo 4

(c) Supondo que a = 0,02   m , b = 0,018   m e i = 100   A , teremos o campo magnético com r variando

B r = { 0 ,  

                                                                        2,28 × 10 - 4 ,  

                                                                          7,66 × 10 - 13 ,  

                                                                          2,95 × 10 - 12   }

Resposta

  1. B = μ 0 i 2 π r   r 2 - b 2 a 2 - b 2
  2. B = μ 0 i 2 π a

B r = { 0 ,  

                                                                        2,28 × 10 - 4 ,  

                                                                          7,66 × 10 - 13 ,  

                                                                          2,95 × 10 - 12   }

Exercícios de Livros Relacionados

A figura 29-66 mostra uam seção reta de um fio cilíndrico longo de raio a = 2,00c m que conduz uma corrente uniforme de 170A . Determine o móulo do campo magnético produzido pela corrente a uma distân
A Fig. 31-58 mostra uma seção transversal de um condutor cilíndrico longo, de raio a, contendo um buraco cilíndrico longo de raio h. Os eixos dos dois cilindros são paralelos e estão separados por uma
A Fig. 31-56 mostra uma seção transversal de um condutor longo de um tipo chamado de cabo coaxial. Seus raios (a. b, c) são mostrados na figura. Existem correntes iguais i mas de sentidos opostos nos
A Fig. 31 -59 mostra uma seção transversal de uma chapa condutora infinita com uma corrente por unidade de comprimento A emergindo perpendicularmente do plano da página. (a) Use a lei de Biot-Savart e