80- Em uma região do espaço onde não há nenhuma corrente de condução e nenhuma corrente de deslocamento, é impossível existir um campo magnético que caia repentinamente para zero. Para comprovar essa afirmação, use o método da contradição. Suponha que esse caso seja possível; a seguir, mostre que essa hipótese contradiz alguma lei da física.
Na metade inferior de uma folha de papel, desenhe linhas paralelas igualmente espaçadas para representar um campo magnético uniforme orientado da esquerda para a direita. Use linhas tracejadas para desenhar um retângulo com o lado horizontal dentro do campo magnético e com o lado horizontal na parte superior da folha, em que .
Mostre que a integração ao longo desse retângulo entra em contradição com a lei de Ampere.
Passo 1
Vamos começar desenhando o que se diz na letra .
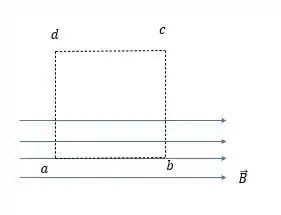
Onde a linha vai estar na área onde existe um campo magnético de intensidade e com sentido da esquerda para a direita e o lado está fora desse campo magnético.
Vamos supor que os lados desse quadrado valem
Passo 2
Agora vem a questão de fato, vamos supor que o campo magnético em seja igual a pela campo magnético que ela está inserida e o campo magnético em seja pelo mesmo motivo.
A lei de Ampere nos diz que:
E por ser um produto escalar logo a lei de Ampere somente nos diz respeito quando ao produto de linhas que estão paralelas. Dessa forma as linhas e não gerando nenhum resultado. E a integral fechada nos diz respeito a integral da superfície fechada , logo a integral fica:
Ou:
Só que assumimos que o lado e , o que contradiz a Lei de Ampere.