Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 56

Na Figura 24.9ª, considere , e . Suponha que os capacitores carregados sejam desconectados da fonte e desconectados um do outro; a seguir, eles são novamentes ligados em si, porém através das placas com cargas opostas. O quanto a energia do sistema diminui?

Passo 1

Okaay!! Here we go! Inicialmente os capacitores estão conectados em pararelo com a fonte e podemos calcular as cargas e de boas. Depois que eles são reconectados juntos, a carga total é:

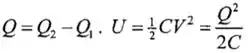
Passo 2

Depois que elas estão recnoectadas, as cargas se adicionam e as tensões são as mesmas, logo:

Para o sistema em pararelo. Originalmente:

A energia armazenada inicialmente é de:

Passo 3

Desconectando e virando os capacitores, agora a carga total é de

E a capacitância equivalente é a mesma. Agora a energia armazenada é de:

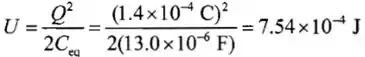
A mudança na energia armazenada é de:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera condutora isolada de raio R tem carga Q distribuída uniformemente sobre sua superfície. Determine a distância R ' do centro da esfera tal que metade da energia eletrostática total do sistem

Um capacitor esférico é composto de uma esfera interna que tem raio R 1 e carga + Q , e uma fina casca esférica concêntrica que tem raio R 2 , e carga - Q . (a) Determine o campo elétrico e a densidad

Uma esfera metálica de raio igual a 0,50c m está imersa no ar. Sabendo-se que a rigidez dielétrica do ar à pressão atmosférica vale 3 k V / m m , qual é a carga máxima que se pode colocar na esfera pa

Um capacitor de placas pararelas está imerso no ar, cuja rigidez vale 3 k V / m m . (A) Mostre que a energia potencial máxima que pode ser acumulada no capacitor somente depende do volume do espaço in

Calcule:a) a capacitância de um par de placas paralelas com área de 100c m 2 cada, separadas de 3,0m m ;b) o campo elétrico quando o capacitor possui uma carga de 0,10μ C .