Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 86

86- Modelo de Quark para o nêutron. O nêutron é uma partícula com carga elétrica igual a zero. Contudo, ele possui um momento magnético diferente de zero, cujo componente z é igual a 9.66 × 10 - 27   A m 2 . Esse momento pode ser explicado pela estrutura interna do nêutron. Diversas evidências indicam que o nêutron é composto de três partículas fundamentais, chamadas de quarks: um quark ‘up’ ( u ) , com carga + 2 e / 3 , e dois quarks ‘down’ ( d ) , cada um com carga - e / 3 . A combinação dessas três cargas produz uma carga total + 2 e 3 - e 3 - e 3 = 0 .

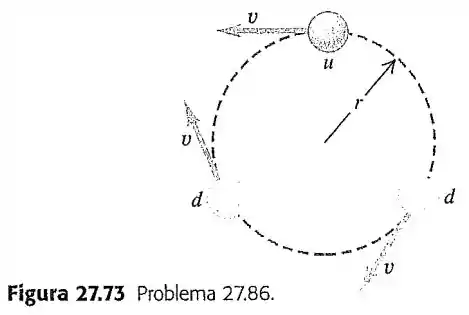
Caso os quarks estejam em movimento, eles produzem um movimento magnético diferente de zero. Com um modelo muito simples suponha que o quark ( u ) se mova em uma órbita circular em sentido anti-horário e que os dois quarks ( d ) se movam no sentido horário, todos os quarks se movendo com o mesmo módulo da velocidade v ao longo das circunferências de mesmo raio r (Figura 27.73 ).

( a ) Obtenha a corrente elétrica produzida pela circulação do quark ( u ) .

( b ) Determine o módulo do momento magnético oriundo da circulação do quark u .

( c ) Determine o módulo do momento magnético do sistema constituído pelos três quarks. (Tome cuidado e use os sentidos corretos para os momentos magnéticos.)

( d ) Com que velocidade v os quarks devem se mover para reproduzir o valor do momento magnético do nêutron? Use o valor r = 1.2 × 10 - 15   m (o raio do nêutron) para o raio das órbitas.

Passo 1

A corrente elétrica em relação a variação da carga é obtida por:

d Q = I d t

Logo :

I = d Q d t

Onde a carga de um up é de 2 e 3 e o tempo de circulação desse up com uma velocidade v em um círculo de raio r (dados do final do enunciado e da figura) será de:

v = 2 π r t → t = 2 π r v

Então temos:

I = 2 e 3 2 π r v = 2 e v 6 π r = e v 3 π r

Passo 2

O momento magnético por ter unidade de medida A m 2 tem uma fórmula do tipo:

μ = I A

Sem nenhuma constante atrelada a ele, então para a área do círculo igual a π r 2 teremos:

μ = e v 3 π r × π r 2 = e v r 3

Passo 3

Como os outros quarks tem metade da carga então a corrente gerada por um up será de:

I = e 3 2 π r v = e v 6 π r

E momento magnético igual a:

μ = e v 6 π r × π r 2 = e v r 6

Sem destinção de sinal, somente o valor escalar de todos eles.

Então o momento magnético total será de:

μ t = e v r 3 + e v r 6 + e v r 6 = 2 e v r 3

Passo 4

Como foi calculado o momento magnético dos três quarks em conjunto, então vamos utilizar-lo para calcular a velocidade total para que ele tenha o momento magnético do nêutron.

μ = 2 e v r 3 → v = 3 μ e r

v = 3 × 9.66 × 10 - 27 2 × 1.6 × 10 - 19 × 1.2 × 10 - 15   = 75.47 × 10 6   m / s

Resposta

a )   I = e v 3 π r

b )   μ = e v r 3

c ) μ t = 2 e v r 3

d )   v = 75.47 × 10 6   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro fios longos, retilíneos e paralelos, conduzem corrente I. Em um plano perpendicular aos fios, eles estão nos vértices de um quadrado de lado a. Determine a magnitude da força por unidade de com
Três fios longos e paralelos estão nos vértices de um quadrado, como mostrado na Figura 27-54. Cada fio conduz uma corrente I. Determine o campo magnético no vértice não ocupado do quadrado quandoa) T
Cinco fios longos, retilíneos e condutores são paralelos ao eixo z e cada um conduz corrente I na direção +z. Cada um dos fios está a uma distância R do eixo z. Dois dos fios interceptam o eixo x, um
Exercício de Livro
Exercício de Livro