Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 9.Exercícios e Problemas - Ex. 12

9.12P* Seja m a massa da tábua do balanço da figura 9.19. A) Qual é o momento de inércia do sistema em relação ao ponto de apoio? B) Qual é a aceleração angular inicial do sistema?

Passo 1

Belezoca galerinha, a figura 9.19 é igual a do exercício anterior, dada como:

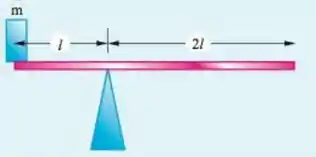
Só que dessa vez a massa da tábua já é conhecida, ela é igual a massa m do bloco. Então pra gente calcular o momento de inércia, podemos usar a fórmula:

I = m i r i 2

E pra facilitar nosso cálculo, podemos dividir em o momento de inércia total em 3 momentos de inércia, um para o bloco, e o os outros dois são para as respectivas divisões da tábua, tal que:

I = m l 2 + m 3 l 2 + 2 3 m 2 l 2 2

I = m l 2 + m 3 l 2 + 2 3 m l 2

Portanto o momento de inércia total é:

I = 2 m l 2

Passo 2

Belezoca, agora queremos encontrar a aceleração angular α que o sistema possui, e pra isso podemos usar a relação entre o torque τ e o momento de inércia, dado por:

τ = I × α

Então bora descobrir o torque resultante dessas forças, pra isso podemos novamente calcular separadamente cada torque que cada parte exerce, tal que:

∑     τ = m l g + m 3 l 2   g - 2 m 3 . 2 l 2 g  

∑     τ = m l g + m l 6 - 2 m l 3 g

Tal que o torque resultante é dado por:

∑     τ = m l g 2

Logo se a gente igualar esse resultado a nossa expressão inicial, temos que:

τ = I × α

m l g 2 = 2 m l 2 × α

Dessa forma a aceleração angular será:

α = m l g 4 m l 2

α = g 4 l

Resposta

  1. I = 2 m l 2
  2. α = g 4 l
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O raio de um pequeno carrossel é 2,2 m . Para iniciar a rotação, você enrola uma corda em torno de seu perímetro e puxa com uma força de 260 N , durante 12 s . Durante este tempo, o carrossel completa
Durante um jogo de sinuca, a tacadeira (uma esfera uniforme de raio r ) está em repouso sobre a mesa horizontal. Você atinge a bola horizontalmente com o taco, que aplica uma intensa força horizontal
Uma esfera maciça e uniforme é posta a girar em torno de um eixo horizontal com uma rapidez angular ω 0 e, então, é colocada sobre o piso, com seu centro de massa em repouso. Se o coeficiente de atrit
Uma bola de bilhar, de 0,16 k g , cujo raio vale 3,0 c m , recebe uma forte tacada. A força aplicada é horizontal e sua linha de ação passa pelo centro da bola. A rapidez da bola imediatamente após a
Um disco uniforme de 5,0 k g tem um raio de 0,12 m e gira livremente em torno de seu eixo. Um cordão, enrolado em volta do disco, é puxado com uma força de 20 N . (a) Qual é o torque exercido por esta