Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 103

Uma esfera maciça e uniforme é posta a girar em torno de um eixo horizontal com uma rapidez angular ω 0 e, então, é colocada sobre o piso, com seu centro de massa em repouso. Se o coeficiente de atrito cinético entre a esfera e o piso é μ c , determine a rapidez do centro de massa da esfera quando ela começa a rolar sem deslizar.

Passo 1

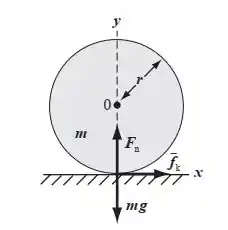
Galera, aqui se a esfera roda, só tem uma força que é capaz de ser a causa disso. É a força de atrito, porque é a única que atua na direção tangencial. A gente pode ver isso pelo diagrama de forças, ó:

Passo 2

Vamos começar aplicando a segunda lei de Newton:

f a t = m a

F n = m g → f a t = μ c m g = m a → a = μ c g

Para a rotação:

∑ τ = f a t r = I α

m a r = 2 5 m r 2 α

α = m a r 2 5 m r 2 = 5 2 × a r = 5 μ c g 2 r

Passo 3

Relacionamos a velocidade angular com a aceleração angular pela equação:

ω = ω 0 - α t

ω = ω 0 - 5 μ c g t 2 r

Lá da cinemática, a gente sabe que, partindo do repouso, v = a t , e aqui, v = μ c g t .

Se o corpo rola sem deslizar, v = ω r !

μ c g t = ω 0 - 5 μ c g t 2 r r

ω 0 r = 7 μ c g t 2

t = 2 r ω 0 7 μ c g

Passo 4

Voltando na equação v = μ c g t , obtemos:

v = μ c g 2 r ω 0 7 μ c g

v = 2 r ω 0 7

Resposta

v = 2 r ω 0 7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra horizontal fina de comprimento l e massa M é articulada em torno de um eixo vertical passando em sua extremidade. Uma força com módulo constante F é aplicada à outraextremidade, fazendo a ba
O volante de certa máquina possui momento de inércia igual a 2,50k g ⋅ m 2 em torno do seu eixo de rotação. Qual é o torque constante necessário para que, partindo do repouso, sua velocidade angular a
Uma casca esférica uniforme de 8,40 kg e 50,0 cm de diâmetro possui quatro pequenas massas de 2,0 kg presas à superfície externa e igualmente espaçadas entre si. Esse sistema está girando em torno de
Um balde com água de 15,0k g é suspenso por uma corda enrolada em torno de um sarilho, constituído por um cilindro sólido com diâmetro de 0,300m e massa igual a 12,0k g . O cilindro é pivotado sobre u
A peça de uma máquina tem o formato de uma esfera maciça e uniforme com massa de 225 g e diâmetro de 3,0 cm. Ela está girando em torno de um eixo com atrito desprezível que passapelo seu centro, mas e