9.16P Suponha que a haste vista na Figura 9.20 não sinta nenhum atrito com a superfície de apoio e que sua queda inicie do repouso a partir da posição vertical. A) Em que ponto cai o centro de massa da haste? B) Qual é a velocidade angular da haste em relação ao seu centro de massa imediatamente antes do fim da queda?
Passo 1
Belejóia galera, como vimos no exercício anterior, a força de atrito não era responsável pelo deslocamento do centro de massa, MAAASS era ele quem anulava a força peso no “eixo da haste” obrigando o torque resultante da força a peso deslocar o centro de massa:
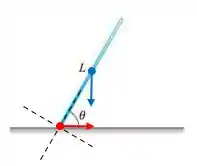
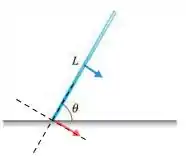
Só que agora não temos atrito, então a única força atuando é a força peso:
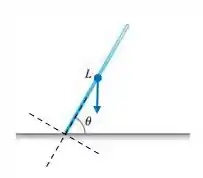
Dessa forma o centro de massa irá cair necessariamente no ponto abaixo dele mesmo.
Passo 2
Belezoca, já na letra (B), pra gente descobrir a velocidade angular, podemos usar a conservação da energia mecânica:
De forma que a energia inicial, é dada pela energia potencial da altura que o centro de massa se encontra quando está na vertical:
Enquanto a energia mecânica final é formada pela mistura de energia cinética de translação com energia cinética de rotação:
Onde é o momento de inércia, dessa vez em relação ao uma rotação em torno do centro de massa , enquanto pode ser escrito em função da velocidade angular e da distância do centro de massa até a extremidade, tal que:
Dessa forma podemos reescrever nossa energia mecânica final como:
Passo 3
Portanto se a gente igualar as energias, vamos obter:
E isolando a velocidade angular, temos: