Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 9.Exercícios e Problemas - Ex. 21

9.21P Uma roda de bicicleta tem aro externo com 30   cm de raio e massa igual a 800   g , e 72   hastes radiais com massa de 10   g cada uma. Supondo que o aro interno tenha massa e raio desprezíveis, calcule o momento de inercia da roda em relação ao seu eixo.

Passo 1

Belezoca galerinha, como estamos tratando de vários corpos distintos, como o aro e as hastes, podemos calcular separadamente o momento de inércia de cada um deles e depois somar tudo. De forma que o momento de inércia de um aro é dado pra gente de acordo com a tabelinha como:

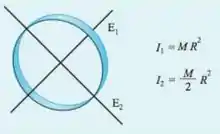
No nosso caso o eixo de rotação passa pelo centro do aro, de forma que o momento de inércia dele é:

I A = M A R 2

Já para as hastes, temos 72 delas girando todas ao redor de sua extremidade, de acordo com nossa tabela, o momento de inercia de uma haste é:

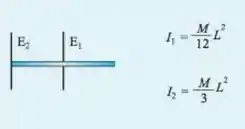
Logo para 1 haste, temos que:

I H = M H 3 L 2

Maaass como estamos falando de 72 hastes e tamanho L delas coincide com o raio R do aro, temos:

I H = 72 3 M H R 2

I H = 24 M H R 2

Passo 2

Portanto o somatório dos momentos de inércia é:

I = I A + I H

I = M A R 2 + 24 M H R 2

Logo se a gente substituir os valores que o enunciado nos fornece, obtemos que:

I = 0,8 0,3 2 + 24 0,01 0,3 2

I = 0,0936   kg.m²

Resposta

I = 0,0936   kg.m²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A molécula de oxigênio ( O 2 ) tem uma massa de 5,30 × 10 - 26k g e um momento de inércia de 1,94.10 - 46k g ∙ m 2 em relação a um eixo que passa pelo ponto médio da reta que liga os dois átomos e é p
9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.
9.7P Calcule o momento de inércia da régua fina mostrada na figura 9.17 em relação ao eixo E .
10.15P Calcule o momento de inércia de uma porta de largura D e massa M em relação ao eixo que passa pelas dobradiças.