Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 9.Exercícios e Problemas - Ex. 5
9.5P A figura 9.16 mostra um disco de massa e o momento de inércia caindo sob o efeito da gravidade. Além disso da velocidade de queda, o disco tem uma velocidade angular . A) qual é o torque que a gravidade exerce sobre o disco em relação a um ponto sobre a linha vertical sólida? B) Para qual velocidade o momento angular do disco em relação a um ponto sobre a linha sólida é nulo?
Passo 1
Show de bolinhas galera, na letra (A) queremos encontrar o torque que a gravidade exerce sobre o disco em relação a linha sólida, à uma distância de metros como mostrado na figura:
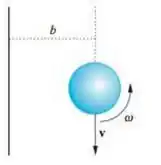
Dessa forma, podemos lembrar que o torque é calculado pela fórmula:
Onde é o raio perpendicular a força de atuação e ao eixo referencial, dado por , e por outro lado a força é força gravitacional que age sobre o disco, dada por:
Portanto o torque gerado é:
Passo 2
Já na letra (B), queremos saber qual velocidade faz com que o momento angular em relação ao eixo de linha sólida seja nulo. Pra isso podemos lembrar que o momento angular que o disco já possui é relacionado a sua velocidade angular, dada por:
Onde é o momento de inércia do disco equanto é sua velocidade angular. MAAASSS, o momento angular gerado momento linear do disco é dada por:
Onde , e o raio é novamente a distância até o eixo, tal que:
E como o momento deve ser nulo, temos que:
Logo:
Portanto a velocidade será: