Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.Problemas Adicionais - Ex. 97
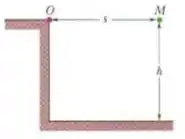
Uma partícula de massa é liberada de um ponto que está a uma altura acima do solo e a uma distância de um ponto de observação , como mostra a figura. Qual é o módulo do momento angular da partícula em relação a quando a partícula percorreu metade da distância até o solo?
Passo 1
Quando a partícula é liberada a partir do repouso, ela terá uma velocidade na vertical para baixo certo?
Isso quer dizer que a sua velocidade sempre será perpendicular à distância entre o ponto inicial de e a origem . Então podemos usar a seguinte fórmula para calcular o módulo do momento angular:
Onde é a distância perpendicular até o ponto , ou seja, :
Passo 2
E para calcular a velocidade depois de cair por uma altura , vamos usar essa fórmula aqui:
E então o momento angular é:
Resposta
O módulo do momento angular é .