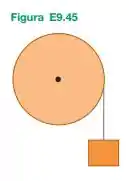
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda, que é de . Depois você monta a roda, usando mancais livres de atrito, sobre um eixo horizontal que passa pelo centro da roda. Você enrola uma corda leve em volta da roda e pendura um bloco de madeira de na extremidade livre da corda, como indica a Figura E9.45. Você libera o sistema do repouso e descobre que o bloco desce em Qual é o momento de inércia da roda para esse eixo?

Para o bloco que está caindo, as únicas forças que agem sobre ele são a tensão (vertical para cima) e o peso (vertical para baixo) e aplicando a segunda lei para translação temos

E daqui podemos determinar qual é a tração com que o fio gira a roda! Mas pera lá, não temos a aceleração! Só que o problema nos deu a distância que ele percorre e o tempo, sabendo que o bloco partiu do repuso vamos achar a aceleração

Tranquilo? Agora sim podemos encontrar a tensão

Tudo bem até aqui?

Agora como temos a força causadora do torque, podemos aplicar a segunda lei (para rotações) na roda! O torque nela é

Sabendo que , e como o diâmetro é sabemos que o raio é A aceleração foi calculada no passo anterior. E o torque? Torque é o produto vetorial entre a força e o braço de alavanca, que é a medida da distância entre a linha de atuação de força e o pontode giro (que no nosso caso é o raio da roda), aí temos

Simplificando temos

Esse é o nosso momento de inércia!