Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 62
9.62. Nos problemas de 62 a 65, lhe é fornecida a equação a ser usada para resolver o problema. Em cada uma delas, você deve
a. Redigir um problema realista para qual esta equação seja correta.
b. Resolver o problema elaborado, incluindo uma representação pictórica.
62.
Passo 1
Nesse exercício a gente tem um corpo de que em um momento tinha velocidade e em outro momento tinha velocidade .
A gente pode ver, pela a equação que esse é um problema trata do teorema impulso-momento. A gente tem a variação de um momento linear sendo igualado ao cálculo de um impulso.
Um possível enunciado seria: “Um disco de hockey de está indo para esquerda à , quando um jogador acerta a bola com seu taco fazendo ela ir na direção oposta a uma velocidade de . A força com que o jogador atinge a bola com o taco é dado pelo gráfico:
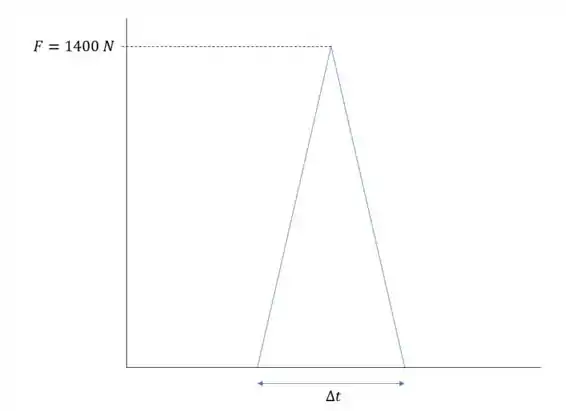Qual é o tempo máximo que o taco pode ficar em contato com o disco?”
Passo 2
Agora vamos para o item “b”. Vamos fazer a representação pictórica.
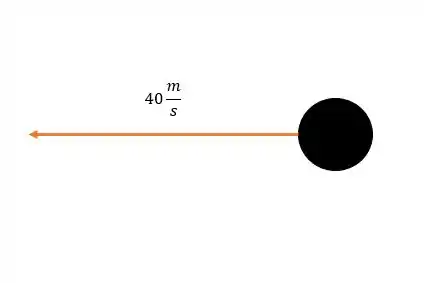
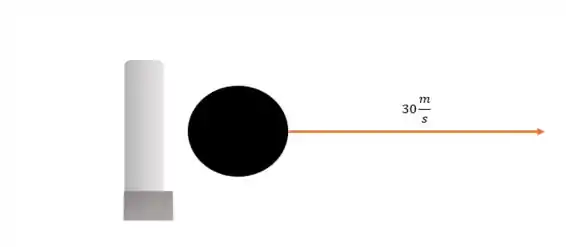
Vamos assumir o sentido positivo para a direita. Bom a gente pode usar o teorema que diz que a variação do momento é igual ao impulso
Bom, a gente tem um gráfico de força por tempo, o impulso é a área embaixo desse gráfico, logo
Substituindo os valores
Vamos isolar a variação de tempo
Esse é o tempo de contato entre o disco e o taco.
Resposta
Ei, a resposta está no passo a passo :)