Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 71
9.71. Você é o diretor de voo em Terra de um foguete científico de 2000 kg que se aproxima de Marte a 25000 km/h. Ele deve rapidamente baixar sua velocidade para 15000 km/h a fim de iniciar uma descida controlada até a superfície. Se o foguete entrar na atmosfera marciana com muita velocidade, ele queimará completamente, e se entrar lento demais, terá de consumir seu combustível em manobras antes de se aproximar da superfície e acabará se chocando com ela. O foguete tem um novo sistema de freagem: várias “balas” de 5,0 kg cada uma podem ser disparadas diretamente para a frente. Cada uma delas possui uma carga altamente explosiva que a impulsiona a 139000 km/h em relação ao foguete. Você precisa enviar ao foguete uma instrução para que ele dispare o número de balas desejado. O sucesso da empreitada lhe trará fama e glória, todavia o fracasso da missão de 500 milhões de dólares significará a completa ruína de sua carreira.
Passo 1
O modelo do foguete é o seguinte:
E aí para frear o foguete dispara balas para frente:
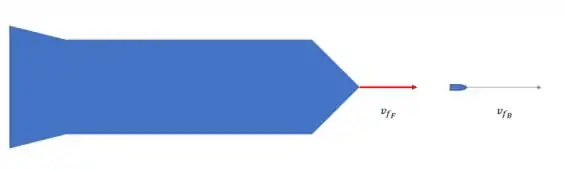
A cada bala que o foguete dispara, o foguete perde , já que a bala é expelida do foguete e pesa .
Outra coisa importante que temos que notar é a velocidade com que a bala é disparada, ela tem em relação ao foguete, matematicamente
Passo 2
Vamos usar a conservação de momento para uma bala.
O momento inicial é o momento do foguete, o momento final é a soma dos momentos do foguete e da bala.
Se a gente conseguir calcular a diferença de velocidade que uma bala causa no foguete, seremos capazes de deduzir quantas balas são necessárias para o foguete parar. A gente achou uma equação para , vamos substituir na equação de conservação de momento.
Agora vamos reorganizar a equação
Agora a gente pode fazer o seguinte
Então
Passo 3
Beleza, agora a gente sabe quanto de velocidade diminui quando uma bala é disparada. O problema é que depois que essa bala é disparada a massa do foguete diminui. Então a variação de velocidade vai ser diferente. Mas, como a bala tem apenas e o foguete tem , essa diferença pode ser desprezada, e a massa do foguete pode ser considerada constante. Sendo assim, se a gente supor que cada bala diminui exatamente de velocidade, a gente pode calcular quantas balas são necessárias para desacelerar o foguete para ele pousar com segurança, ou seja, diminuir a velocidade para . Como o foguete está inicialmente à , o foguete tem que diminuir .
Podemos calcular o número de balas assim