Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 68

9.68. Uma bola de madeira de 20 kg está suspensa por um fio com 2,0 m de comprimento. A máxima tensão que o fio pode suportar sem se romper é de 400 N. Um projétil de 1,0 kg, deslocando-se horizontalmente, colide com a bola e fica incrustado na madeira. Qual é o máximo valor de velocidade que o projétil pode possuir sem que o fio se rompa na colisão?

Passo 1

Bom, vamos começar fazendo um desenho da situação.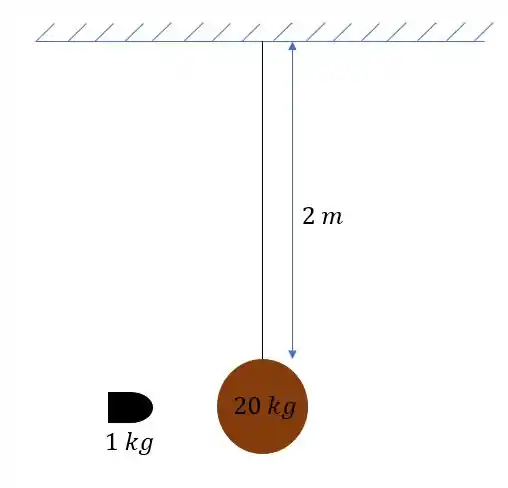

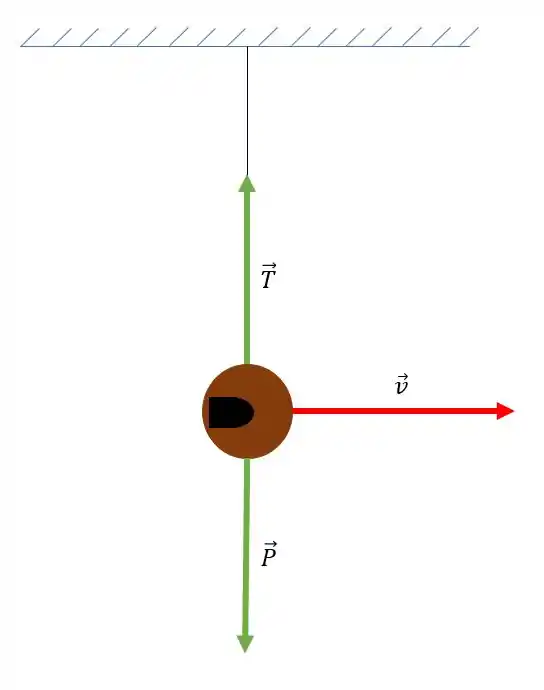
Nós temos uma colisão inelástica nesse problema. Nós queremos descobrir a velocidade inicial do projétil. Para isso nós podemos usar conservação de momento. Então temos que

p T i = p T f

Bom, o momento inicial será o momento do projetil somado com o momento da bola. O momento final é o momento do objeto que ser forma quando o projetil atinge a bola, esse objeto tem massa igual a soma das massas do projetil e da bola. Matematicamente temos que

p T i = p T f

Equivale à

m p v p i + m b v b i = m p + m b v f

O índice “ p ” é do projetil e o índice “ b ” é da bola. A velocidade inicial da bola é 0 , já que ela está parada, então temos

m p v p i = m p + m b v f

Passo 2

Nós podemos começar descobrindo a velocidade final máxima possível. Para fazer isso a gente precisa usar a segunda lei de Newton para o movimento circular, fica o seguinte

T - P = m p + m b v f 2 r

Assumindo para cima como sentido positivo.

Então temos

T - m p + m b g = m p + m b v f 2 r

Agora a gente pode isolar a velocidade final

v f 2 = T - m p + m b g r m p + m b

Então

v f 2 = T r m p + m b - g r

Passando a raiz

v f = T r m p + m b - g r

Essa é a velocidade final máxima, qualquer velocidade acima dessa o movimento circular é impossível, o cabo quebra.

Passo 3

Agora que temos a velocidade final, podemos calcular a velocidade inicial do projetil. Vamos voltar a equação

m p v p i = m p + m b v f

Agora a gente isola a velocidade inicial

v p i = m p + m b v f m p

Agora a gente substitui o valor da velocidade final

v p i = m p + m b m p T r m p + m b - g r

Agora a gente tem tudo para calcular a velocidade inicial do projetil, só falta substituir os valores

v p i = 20 + 1 1 400 2 1 + 20 - 9,81 2

Fazendo essa continha chegamos em

v p i = 90,26 m s ≈ 90 m s

Essa é a velocidade máxima que o projetil pode atingir a bola de madeira sem quebrar o cabo.

Resposta

90 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Durante a madrugada, um carro de luxo, de massa total igual a 2400 Kg, bate na traseira de um carro de massa total 1200 kg, que estava parado num sinal vermelho. O motorista do carro de luxo alega que
Um caminhão carregado, com massa total de 3 toneladas, viajando para o norte a 60 km/h, colide com um carro de massa total 1 tonelada, trafegando a leste a 90 km/h, num cruzamento. Calcule em que dire
Um disco circular de raio a, que se desloca sobre um colchão de ar com velocidade v e atrito desprezível, colide com um disco idêntico em repouso. O parâmetro de choque é b. a) Considere a colisão no
Considere um sistema qualquer de duas partículas, de massas m 1em 2 velocidades v 1ev 2 . Sejam T 1eT 2 as energias cinéticas das duas partículas, e v r , a velocidade relativa da partícula 2 em relaç
Um átomo de hidrogênio, movendo com velocidade v, colide com uma molécula de hidrogênio em repouso, sofrendo uma deflexão de 45 ° . Calcule: a) a magnitude da velocidade do átomo após a colisão; b) a