Em abril de 1974, o belga John Massis conseguiu puxar dois vagões de passageiros mordendo um freio preso por uma corda aos vagões e se inclinando para trás com as pernas apoiadas nos dormentes da ferrovia. Os vagões pesavam (cerca de toneladas). Suponha que Massis tenha puxado com uma força constante de módulo vezes maior que seu peso e ângulo de com a horizontal. Sua massa era e ele fez os vagões se deslocarem de . Desprezando as forças de atrito, determine a velocidade dos vagões quando Massis parou de puxar.

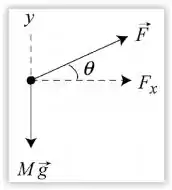
Entõa pessoal , bora dar uma olhada no diagrama de corpo livre do sistema. A força exercida por John Massis foi :

Como o movimento foi na horizontal, a Segunda Lei de Newton nos dá , em que é a massa total dos dois vagões. Assim, a aceleração dos vagões é de