Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 2.Problemas - Ex. 46
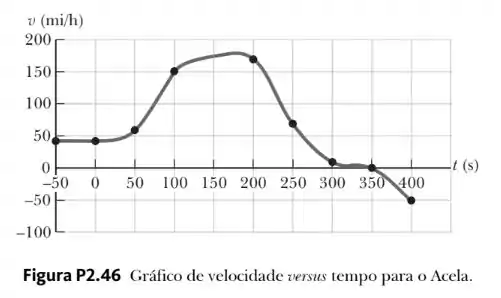
O Acela é um trem elétrico na linha Washington-Nova York-Boston, carregando passageiros a . Um gráfico velocidade-tempo para o Acela é mostrado na Figura P2.46.
- Descreva o movimento do trem em cada intervalo de tempo sucessivo.
- Encontre o pico de aceleração positiva do trem no movimento traçado no gráfico.
- Encontre o deslocamento do trem em milhas entre e .
Passo 1
Opaaaa... belezinha???
Nessa questão temos esse gráfico de velocidade por tempo.
Na letra (a) é pedido para descrever o movimento, então vamos analisar onde é contrante, onde aumenta, onde diminui e tal tal...
Já na letra (b) vamos precisar achar o pico de aceleração positiva e o que pode ajudar é a equação:
E a representação disso, da derivada, são as linhas tangentes que a gente pode traçar no gráfico. Se a gente calcular a inclinação nessa reta tangete temos a aceleração.
Para a letra (c) vamos calcular a área do gráfico de 0 até 200 segundos pra achar o deslocamento.
Então bora lá...
Passo 2
- Já começa com uma coisa estranha que é o tempo sendo negativo (o que não existe, né, teoricamente), mas pode ser algum erro =X
- Repara que o movimento só tem aceleração positiva de 50 até 170. Se liga só nesse recorte da figura com algumas retas tangentes:
- Agora pra calcular o deslocamento vamos calcular a área do gráfico. Pra isso vamos precisar dar umas aproximadas com retas, tipo assim:
Então vamos começar analisando do 0 para não pesar a consciência.
De 0 até 30, mais ou menos, a velocidade praticamente não muda, então podemos considerar que o trem está andando numa velocidade constante e igual a .
De 30 até 180, mais ou menos, a velocidade vai aumentando, né? Então nesse intervalo de tempo vamos ter um movimento acelerado.
De 180 até 300 muda e a velocidade vai caindo até 0, então temos um movimento desacelerado (com aceleração negativa). O trem está freiando, né... até parar, que é quando a velocidade é igual a 0.
De 300 até 350 tem a velocidade constante e igual a zero, então o trem está paradinho.
De 350 até 400 a velocidade fica negativa, ela cai de zero pra -50, mas sabe o que isso quer dizer?? Que o trem começou a andar no sentido contrário ao que vinha andando. E a velocidade não é constante, então o movimento é acelerado.
Passo 3
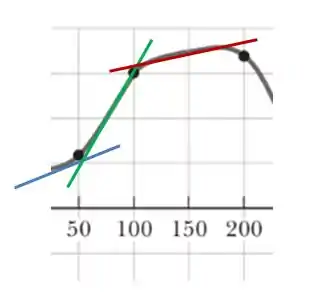
A gente quer o pico da aceleração, então é a maior aceleração possível. E como a gente já sabe que a aceleração vai ser a tangente da reta e isso vai ser a reta mais inclinada, no caso, a verde, né?
CUIDADOOOO... Vamos precisar passar esses segundos pra hora, heim...
(possivelmente o eixo do tempo ta com a unidade errada... não faz muito sentido uma aceleração altíssima dessa pra um trem, né? Hahahaha )
Passo 4
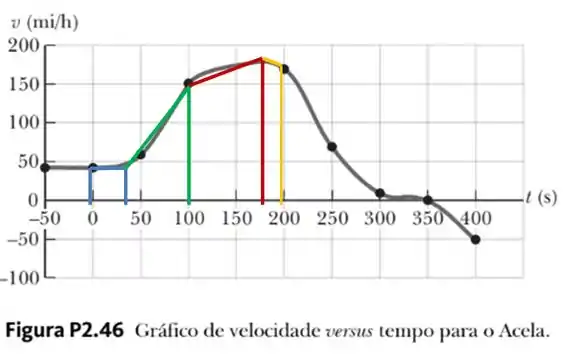
De 0 a 30, a gente vai ter a área do retângulo () :
A gente também vai precisar passar esse segundo pra hora...
De 30 a 100, a gente vai ter a área do trapézio ():
De 100 a 180, outro trapézio:
E de 180 a 200, mais um trapézio:
Agora é só somar essas áreas que encontramos o deslocamento:
Resposta
(b)
(c)