Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 2.Problemas - Ex. 52
Astronautas, em um planeta distante, lançam uma pedra no ar. Com o auxílio de uma câmara que tira fotos a uma taxa constante, eles registram a altura da rocha como uma função do tempo, como dado na tabela seguinte.
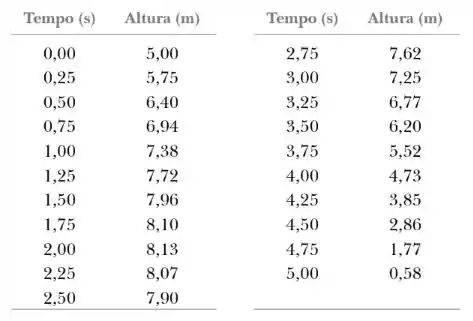
- Encontre a velocidade média da pedra no intervalo de tempo entre cada medição e a próxima.
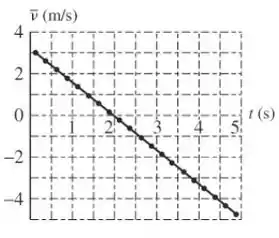
- Usando essas velocidades médias para aproximar os valores da velocidade instantânea no meio desses intervalos de tempo, faça um gráfico da velocidade em função do tempo.
- A pedra se movimenta com aceleração constante? Caso sim, trace uma linha reta de melhor alinhamento no gráfico e calcule sua inclinação para encontrar a aceleração.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
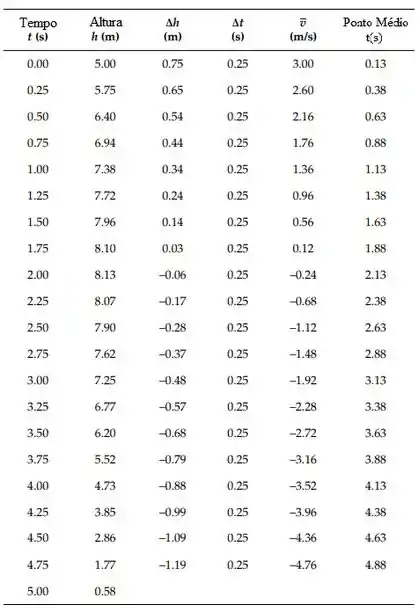
Passo 2
Letra b:
O ajuste muito convincente de uma única linha reta para os pontos no gráfico de velocidade em relação ao tempo indica que a pedra cai com aceleração constante. A aceleração é a inclinação da linha:
Passo 3
Letra c:
Resposta
- Ver tabela
- Ver gráfico
Exercícios de Livros Relacionados
Considere o gráfico da velocidade na figura abaixo. Assumindo x = 0 em t = 0 , escreva as expressões algébricas corretas para x ( t ) , v x ( t ) e a x ( t ) com os valores numéricos apropriados inser
A figura abaixo mostra a aceleração de uma partícula em função do tempo. (a) Qual é a magnitude, em m / s , da área da região sombreada? (b) A partícula parte do repouso em t = 0 . Estime a velocidade
A figura abaixo é um gráfico da velocidade em função do tempo para uma partícula se movendo ao longo de uma linha reta. A posição da partícula em um tempo t = 0 é x 0 = 5,0m . (a) Encontre x para valo
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b
A posição de um corpo oscilando em uma mola é dada por x = A sen ω t , onde A e ω são constantes. A = 5,0c m , e ω = 0,175s - 1 . (a) Plote x como uma função de t para 0 ≤ t ≤ 36s . (b) Meça a incli