Esboce uma curva -- para cada uma das seguintes condições: (a) aceleração é nula e constante enquanto a velocidade é diferente de zero. (b) Aceleração é constante mas não é zero. (c) Velocidade e aceleração são ambas positivas. (d) Velocidade e aceleração são ambas negativas. (e) Velocidade é positiva e aceleração é negativa. (f) Velocidade é negativa e aceleração é positiva. (g) Velocidade é momentaneamente nula mas a aceleração é diferente de zero.
Passo 1
(a) Se a aceleração é sempre nula e a velocidade é diferente de zero, o gráfico da velocidade em função do tempo será simplesmente uma reta horizontal:
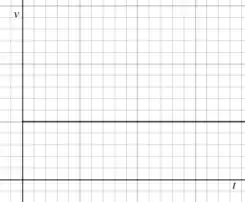
Passo 2
(b) Se a aceleração é constante e diferente de zero, então a aceleração será uma linha reta inclinada, com inclinação igual à aceleração (não sabemos onde o gráfico cruza o eixo , mas como esse é apenas um esboço, isso não será problema):
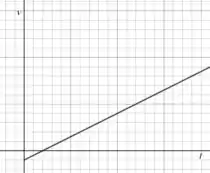
Passo 3
(c) Se velocidade e aceleração são positivas temos um caso muito semelhante ao do item anterior, mas coma garantia de que o gráfico está sempre acima do eixo :
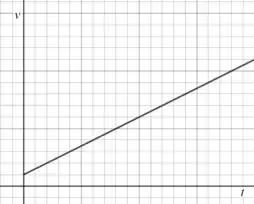
Passo 4
(d) E nesse caso só precisamos inverter todos os sinais do item anterior:
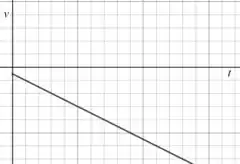
Passo 5
(e) Se a velocidade é positiva e a aceleração é negativa, nós teremos uma reta decrescente que se mantém no primeiro quadrante:
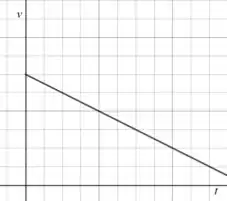
Passo 6
(f) Se a velocidade é negativa e a aceleração é positiva, nós teremos uma reta crescente no quarto quadrante:
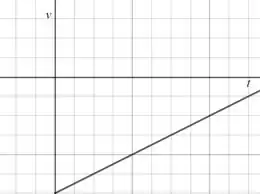
Passo 7
(g) Se a velocidade é momentaneamente nula mas a aceleração é diferente de zero, nos teremos uma reta inclinada (crescente ou decrescente) que cruza o eixo :
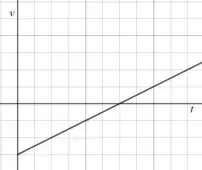
Resposta
Ver gráficos.