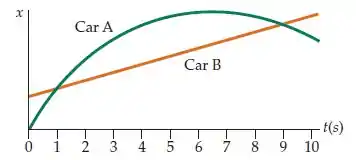
As posições de dois carros em pistas paralelas de um trecho reto de estrada estão plotadas como funções do tempo na figura abaixo. Tome os valores positivos de como estando à direita da origem. Responde qualitativamente às seguintes perguntas: (a) Em algum momento esses dois carros ficam lado a lado? Se sim, indique esse(s) tempo(s) no eixo. (b) Os carros estão sempre viajando no mesmo sentido, ou em parte do tempo eles se movem em sentidos opostos? (c) Em algum momento eles estão viajando à mesma velocidade? Se sim, quando? (d) Em que momento os carros estão mais distantes um do outro? (e) Esboce (sem números) a curva de velocidade em função do tempo para cada carro.
Passo 1
(a) Esse é um gráfico da posição em função do tempo, ou seja, sempre que os dois gráficos se intersectam, nós sabemos que a posição dos dois carros é igual naquele instante de tempo.
Isso quer dizer que os dois carros ficam lado a lado nos instantes e , que são os instantes em que os gráficos se cruzam.
Passo 2
(b) Como podemos saber o sentido em que os carros estão viajando pelo gráfico da posição? É bem simples, se a função da posição for decrescente (velocidade negativa), o carro está viajando no sentido negativo, e vice-versa.
A função do carro é sempre crescente, mas a função do carro começa a decrescer aproximadamente a partir de . Antes disso, os carros se moviam no mesmo sentido.
Passo 3
(c) Olhando para o gráfico da posição em função do tempo, nós podemos saber a velocidade analisando a derivada da função (inclinação da reta tangente ao gráfico).
Imagine uma reta tangente percorrendo a curva do carro , e veja se existe algum momento em que essa reta fica paralela à reta do carro . Quando isso acontecer, as duas retas terão a mesma inclinação, e então os carros tem a mesma velocidade:
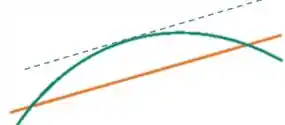
Olhando para o gráfico, isso acontece mais ou menos em torno do .
Passo 4
(d) Como esse é um gráfico da posição em função do tempo, a distância entre os dois carros é dada simplesmente pela diferença nas duas funções:
Olhando para o gráfico podemos ver que a distância entre as duas curvas é máxima mais ou menos em torno de . (A resposta só precisa ser qualitativa, não precisamos nos preocupar com esse valor).
Passo 5
(e) Como falamos antes, a velocidade de cada um dos carros em qualquer ponto é simplesmente a derivada da função naquele ponto.
Como a função da posição do carro é uma linha reta, nós sabemos que a derivada será uma constante, e então o gráfico de é apenas uma linha horizontal.
Já a função da posição do carro é uma parábola (função de segundo grau), e então a derivada será uma função de primeiro grau. E como a parábola tem a concavidade voltada para baixo, a velocidade será negativa.
Então podemos esperar um gráfico mais ou menos assim:
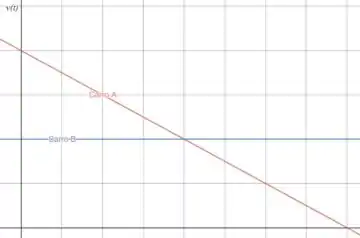
Resposta
(a) Os carros ficam lado a lado em dois instantes.
(b) Em parte do tempo os carros se movem em sentidos opostos.
(c) A velocidade dos dois é a mesma em torno de .
(d) A distância entre os dois é máxima em torno de .
(e) Ver gráfico.