Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 30
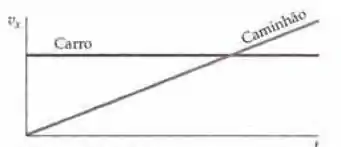
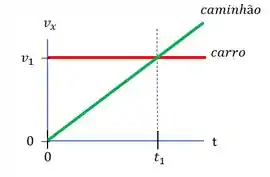
Um carro viajando com velocidade constante passa pela origem no tempo . Nesse instante, um caminhão, em repouso na origem, começa a acelerar uniformemente a partir do repouso. A figura 2-34 mostra um gráfico qualitativo das velocidades do caminhão e do carro como funções do tempo. Compare os deslocamentos (a partir da origem), velocidades e acelerações no instante em que as curvas se intersectam.
Passo 1
O que ele quer é que a gente ache uma relação entre o deslocamento, velocidade e aceleração desses veículos no instante em que as duas retas se cruzam.
Podemos começar relacionando o deslocamento do carro com o deslocamento do caminhão. Como podemos analisá-los em um gráfico da velocidade em função do tempo? Nesse tipo de gráfico, o deslocamento é a área abaixo da reta (ou curva) que descreve o movimento.
Vamos achar uma expressão para o deslocamente do carro. Sendo sua velocidade final e o instante onde seu gráfico se intercepta com o do carro.
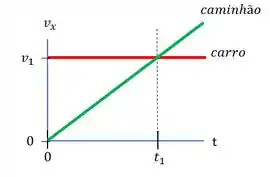
A área abaixo da reta que representa o movimento do carro de até o tempo (reta pontilhada) é a área de um retângulo,
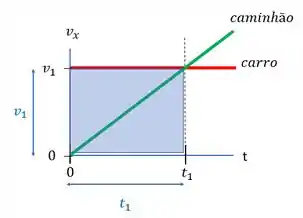
que vale
Esse é o deslocamento do carro. Já o deslocamento do caminhão é a área abaixo da reta inclinada.
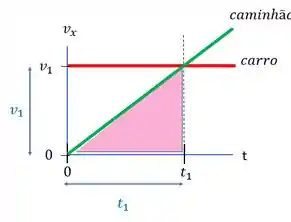
Essa área é um triângulo que vale
Passo 2
Lembra que queremos a relação entre essas duas grandezas? Uma forma de conseguir isso é a dividindo essas expressões que a gente achou, uma pela outra
Dividindo e simplificando
Ou seja, o deslocamento do carro é o dobro do deslocamento do caminhão.
Passo 3
Agora vamos pensar nas velocidades. Essa é a mais fácil, afinal o gráfico do enunciado representa justamente a velocidade em função do tempo.
No instante em que os dois gráficos se cruzam, estamos no mesmo ponto para as duas curvas, certo? Então para as duas vale que e
Logo, a velocidade dos dois veículos é a mesma.
Passo 4
E por fim vamos pensar na aceleração. Quando olhamos para um gráfico da velocidade em função do tempo, a aceleração é a inclinação da reta tangente a esse gráfico. Em outras palavras, a aceleração é a derivada da velocidade em relação ao tempo:
Então para achar informações sobre a aceleração dos nossos veículos, vamos analisar a inclinação das retas que descrevem seu movimento.
Como o gráfico da velocidade do carro é uma linha reta horizontal
Porque seu gráfico fica a todo momento sem inclinação alguma.
Já a do caminhão, por ser uma reta inclinada, tem uma inclinação constante e diferente de zero, assim tem uma aceleração constante e diferente de zero.
Essa aceleração é positiva porque a reta representa sempre um valor crescente de velocidade comforme o tempo passa.
A gente só não tem dado para descobrir o valor da aceleração, tudo bem?
Resposta
No instante em que as duas curvas se intersectam, o deslocamento total do carro é o dobro do deslocamento do caminhão, a velocidade de ambos é a mesma, e a aceleração do caminhão é maior que a do carro.