Qual(is) gráfico(s) (ou nenhum deles) de em função de na figura abaixo melhor descreve o movimento de uma partícula com (a) velocidade positiva e rapidez crescente, (b) velocidade positiva e aceleração nula, (c) aceleração constante diferente de zero, e (d) rapidez decrescente.
Passo 1
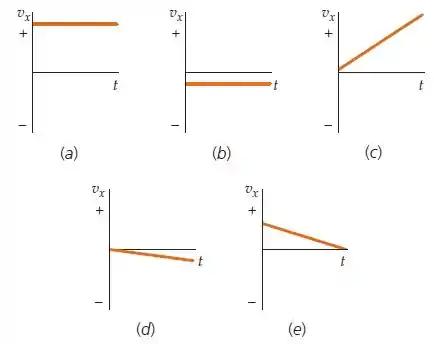
(a) Estamos lidando com um gráfico da velocidade em função do tempo. Isso quer dizer que a velocidade é positiva sempre que a linha do gráfico está acima do eixo .
E o fato de que a “rapidez” é crescente pode ser verificado procurando um gráfico em que o módulo da velocidade seja crescente.
Essas duas condições só são satisfeitas pelo gráfico . Perceba que o gráfico tem rapidez crescente, mas não tem velocidade positiva.
Passo 2
(b) Continuamos com a mesma condição para velocidade positiva, e o fato de a aceleração ser nula indica que a velocidade deve ser constante.
Então estamos procurando por um gráfico que contenha uma linha horizontal acima do eixo . Esse é o caso (apenas) do gráfico .
Passo 3
(c) O fato de que a aceleração é constante e diferente de zero tem a seguinte consequência para o gráfico: ele será um reta inclinada (ou seja, não pode ser horizontal).
Isso acontece porque, nesses casos, a equação para a velocidade é:
Essas condições são satisfeitas apenas pelos gráficos , e .
Passo 4
(d) O fato de que a rapidez é decrescente significa que o módulo da velocidade tem que estar diminuindo no gráfico.
Perceba que embora o gráfico , por exemplo, esteja ficando “mais negativo”, ele não tem rapidez decrescente, porque o módulo está aumentando.
O único gráfico que satisfaz nossa condição é o .
Resposta
(a) Gráfico .
(b) Gráfico .
(c) Gráficos , e .
(d) Gráfico .