Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 45

a)Determine uma expressao para a constante de tase 8no Problema 44 em termos dew,Re C.(b)Qual e o valor deno ω → 0 ? c)Qualeo valor de 5 no ω → ∞ ? d)Explique suas respostas para as Partes(b)e(c).

Passo 1

E ai galera!! Vamos começar aqui essa questão?? Vai ser bem rápido e eu garanto que vocês vão entender!!

O diagrama fasorial para o filtro passa-altas RC é mostrado abaixo. V → app   e  V → R , são os fasores de V i n e V o u t , respectivamente. A projeção de V → a p p no ​​eixo horizontal é V a p p = V i n , e a projeção V → R no eixo horizontal é V R = V o u t .

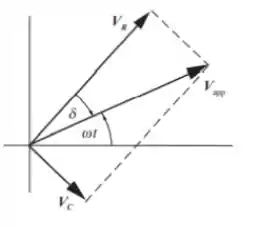
Passo 2

Letra a:

Como V → app  e s t á   a t r a s a d o   d e   ⁡ V → R  em  | δ |

t a n ⁡ δ = - V C V R = - I X C I R = - X C R

Use a definição de X C para obter:

t a n ⁡ δ = - 1 ω C R = - 1 ω R C

Resolvendo para δ , temos:

δ = ∣ t a n - 1 ⁡ - 1 ω R C

Passo 3

Letra b:

Como ω → 0 :

δ → - 90 ∘

Passo 4

Letra c:

Como ω → ∞ :

δ → 0

Passo 5

Letra d:

Para frequências de condução muito baixas, X C > > R e assim   V → c   efetivamente está atrasado de V → in  ∣ em 90 °. Para frequências de condução muito altas, X C < < R e assim V → R está efetivamente em fase com   V → in  .

Resposta

  1. δ = ∣ t a n - 1 ⁡ - 1 ω R C
  2. δ → - 90 ∘
  3. δ → 0
  4. Para frequências de condução muito baixas, X C > > R e assim   V → c   efetivamente está atrasado de V → in  ∣ em 90 °. Para frequências de condução muito altas, X C < < R e assim V → R está efetivamente em fase com   V → in  .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito L C varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Na Fig. 31-27, R = 14,0 Ω , C = 6,20 μ F e L = 54,0 m H e a fonte ideal tem uma força eletromotriz 8 = 34,0V . A chave é mantida na posiçāo a por um longo tempo e depois é colocada na posiçāo b . Dete
Em um circuito L C oscilante, a amplitude da corrente é 7,50 mA, a amplitude da tensão é 250 m V e a capacitância é 220 n F . Determine (a) o período de oscilaçāo; (b) a energia máxima armazenada no c
Em um circuito L C oscilante, L = 3,00 m H e C = 2,70 μ H . No instante t = 0 , a carga do capacitor é zero e a corrente é 2,00 A. (a) Qual é a carga máxima do capacitor? (b) Em que instante de tempo
Um motor elétrico ligado a uma saída de c a de 120V - 60,0H z produz trabalho mecânico na taxa de 0,100h p ( 1h p = 746W ). Sabendo que ele usa uma corrente de 0.650 A (rms), qual é o valor de sua res