Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 116
Um aeromodelo de massa move-se no plano x-y de tal modo que suas coordenadas e variam com o tempo de acordo com e , onde , e .
a) Ache os componentes e da força resultante sobre o plano em função do tempo.
b) Faça um esboço da trajetória do avião entre e e desenhe sobre seu esboço vetores indicando a força resultante para e . Para cada um desses tempos, relacione a direção da força resultante com a direção em que o avião está fazendo a volta, e verifique se o avião está aumentando de velocidade, ou diminuindo de velocidade (ou nenhuma das hipóteses).
c) Qual o módulo e a direção da força resultante para ?
Passo 1
Precisamos lembrar que a aceleração é a segunda derivada da posição. Então se derivarmos duas vezes as equações de movimento dadas, achamos as componentes e da aceleração e daí podemos achar as componentes da força resultante, beleza?
Então a componente da força será:
E a componente :
Passo 2
Vamos calcular a força nos instantes indicados:
- : . A força é puramente vertical para baixo e tem módulo de .
- : . A componente vertical da força resultante continua sendo maior do que a horizontal, mas já é possível identificar uma mudança na trajetória. O avião começa a fazer a curva.
- : . A componente vertical da força resultante quase se equivale a horizontal. A força resultante aponta para o meio da trajetória. O ângulo é próximo de .
- :.
A componente vertical é nula em e vai aumentando em módulo conforme o tempo vai aumentando. Juntando todas essas informações temos o gráfico da trajetória:
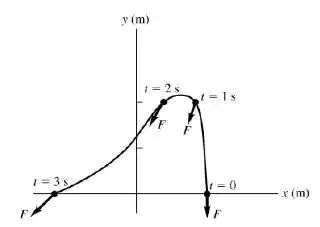
Passo 3
Em já calculamos as componentes no item anterior, e sabemos que a força resultante vai ser dada pela fórmula:
Basta substituir as componentes! Vamos lá?
E a direção? Bom, ela pode ser dada pelo ângulo que a força faz com a origem. Podemos relacionar a tangente do ângulo com as componentes:
Como as componentes são negativas, o ângulo é