Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 89

Um alvo é constituído por uma placa quadrada de madeira vertical com lado igual a 0,250 m e massa de 0,750 kg, pivotada em um eixo horizontal situado em seu topo. A placa é atingida

frontalmente em seu centro por uma bala de massa igual a 1,90 g que se desloca a 360 m/s e que fica retida no interior da placa.

a) Qual é a velocidade angular da placa logo após o impacto da bala?

b) Qual é a altura máxima atingida pelo centro de massa da placa antes que ela comece a oscilar para baixo novamente?

c) Qual deveria ser a velocidade mínima da bala para que a placa completasse a rotação passando a girar em torno do eixo depois do impacto?

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que um alvo é constituído por uma placa quadrada de madeira vertical com lado igual a 0,250   m e massa de 0,750   k g , pivotada em um eixo horizontal situado em seu topo.

A placa é atingida frontalmente em seu centro por uma bala de massa igual a 1,90   g que se desloca a 360   m / s e que fica retida no interior da placa.

Queremos calcular a velocidade angular da placa logo após o impacto da bala e a altura máxima atingida pelo centro de massa da placa antes que ela comece a oscilar para baixo novamente.

Também queremos calcular a velocidade mínima da bala para que a placa completasse a rotação passando a girar em torno do eixo depois do impacto.

Para resolvermos isso, precisamos saber que o momento inicial L 1 é igual ao momento final L 2 (conservação do momento):

L 1 = L 2

Passo 2

A representação desse problema é

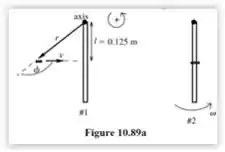
Usaremos a conservação do momento angular à colisão.

Sendo L 1 = L 2 , podemos dizer que

L 1 = m v r sin ⁡ ϕ

L 1 = m v l = ( 1,9 × 10 - 3 k g ) ( 360   m / s ) ( 0,125   m ) = 0,0855   k g × m 2 s

L 2 = I 2 ω 2

Onde m é a massa, v é a velocidade, r sin ⁡ ϕ é metade do alvo, I é o momento de inércia e ω é a velocidade angular.

Sendo o momento de inércia I 2 = I p l a c a + I b a l a = 1 3 M L 2 + m r 2 , então

I 2 = 1 3 M L 2 + m r 2

I 2 = 1 3 ( 0,75   k g ) 0,25   m 2 + ( 1,9 × 10 - 3 k g ) ( 0,125   m ) 2

I 2 = 0,01565   k g × m 2

Passo 3

Igualando L 1 e L 2 :

L 1 = I 2 ω 2

0,0855   k g × m 2 s = ( 0,01565   k g × m 2 ) ω 2

ω 2 = 0,0855   k g × m 2 s 0,01565   k g × m 2

ω 2 = 5,46   r a d / s

Passo 4

Vamos usar conservação de energia para encontrar a altura máxima atingida pelo centro de massa da placa antes que ela comece a oscilar para baixo novamente.

U 1 + K 1 = U 2 + K 2

0 + 1 2 I ω 2 = m g h + 0

Onde K é a energia cinética, U é a energia potencial gravitacional, h é a altura e g é a aceleração da gravidade.

Assim:

h = ( 0,01565   k g × m 2 ) ( 5,46 �� r a d / s ) 2 2 ( 0,75   k g + 1,9 × 10 - 3 k g ) ( 9,8   m / s 2 )

h = 0,0317   m

Passo 5

Para calcularmos a velocidade mínima da bala para que a placa completasse a rotação passando a girar em torno do eixo depois do impacto, podemos utilizar a relação do Passo 2.

1 2 I ω 2 = m g h

ω 2 = 2 m g h I

Nesse caso a altura será de 0,250   m ,

ω = 2 ( 0,75   k g + 1,9 × 10 - 3 k g ) ( 9,8   m / s 2 ) ( 0,250   m ) ( 0,01565   k g × m 2 )

ω = 15,34   r a d / s

Resposta

a) ω 2 = 5,46   r a d / s

b) h = 0,0317   m

c) ω = 15,34   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma roda está girando livremente com uma velocidade angular de 800 r e v / m i n em torno de um eixo cujo momento de inércia é desprezível. Uma segunda roda, inicialmente em repouso e com momento de i
Uma barata de massa m está na borda de um disco homogêneo de massa 4 m que pode girar livremente em torno do centro como um carrossel. Inicialmente, a barata e o disco giram juntos, com uma velocidade
Uma pequena esfera maciça com 0,25 c m de raio e uma massa de 0,56 g rola sem deslizar no interior de um grande hemisfério fixo com 15 c m de raio e um eixo de simetria vertical. A esfera parte do rep
Uma pista é montada em uma grande roda que pode girar livremente, com atrito desprezível, em torno de um eixo vertical (figura abaixo). Um trem de brinquedo de massa m é colocado na pista e, com o sis
Uma barata está no centro de um disco circular que gira livremente como um carrossel, sem torques externos. A barata caminha em direção à borda do disco, cujo raio é R . A figura abaixo mostra a veloc