Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 55

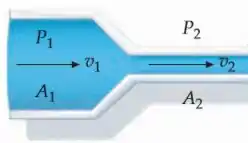
A água flui por um tubo horizontal com velocidade de fluxo igual à v 1 = 3,00 m/s e sob uma pressão P 1 = 200 kPa. Em determinado momento, o diâmetro do tubo pelo qual a água escoa é reduzido pela metade.

a) Qual será a velocidade do fluxo na secção menor?

b) Qual será a pressão na secção menor?

c) Como as taxas de fluxo das duas secções são comparadas?

Passo 1

Para resolvermos a letra a), meus consagrados, iremos fazer uso da equação da continuidade, dada por:

A 1 . v 1 = A 2 . v 2

Onde:

A 1 e A 2 são as áreas das respectivas extremidades;

v 1 e v 2 são as velocidades de fluxo nas respectivas extremidades.

Logo, como queremos saber o valor numérico de v 2 , vamos isolá-lo na equação, meus queridos:

v 2 = v 1 A 1 A 2

Passo 2

Para prosseguirmos, precisaremos lembrar de uma coisinha, já que iremos considerar as extremidades como sendo circulares:

A = π r 2

Como consequência disso:

v 2 = v 1 π r 1 2 π r 2 2

v 2 = v 1 d 1 2 4 d 2 2 4

v 2 = v 1 d 1 d 2 2

Onde: d 1 = 2 d 2

Teremos:

v 2 = v 1 2 d 2 d 2 2

v 2 = 4 v 1

Agora, vamos aplicar os valores dados pela questão:

v 2 = 4 . 3,00

v 2 = 12 m/s

Passo 3

Como consequência do resultado da letra a), iremos responder a letra b) fazendo uso da equação de Bernoulli:

P 1 + p g h 1 + 1 2 p v 1 2 = P 2 + p g h 2 + 1 2 p v 2 2

Notem que a questão nos informa que ambas as extremidades estão à mesma altura, portanto podemos cancelar a expressão p g h de ambos os lados da equação e passamos a ter:

P 1 + 1 2 p v 1 2 = P 2 + 1 2 p v 2 2

Como queremos P 2 , vamos isolá-lo, meus amigos:

P 2 = P 1 + 1 2 p v 1 2 - 1 2 p v 2 2

P 2 = P 1 + 1 2 p ( v 1 2 - v 2 2 )

Lembrando que:

p a = 1.10 3 k g / m 3 (densidade da água);

1atm=101325Pa.

Agora, vamos somente substituir os valores que temos em mãos:

P 2 = 200.000 + 1 2 1.10 3 . ( 3 2 - 12 2 )

P 2 = 200.000 + 1 2 . 1000.135

P 2 = 200.000 - 67.500

P 2 = 132.500 P a = 1,325 . 10 5 P a

P 2 = 1,325.10 2 k P a

Passo 4

Sabemos que, também pela equação da continuidade:

I m 1 - I m 2 = d m 12 d t

Entretanto, a questão nos informa que devemos considerar um fluxo de estado estacionário, logo, essa informação nos assegura que: d m 12 d t = 0

Com isso, teremos que:

I m 1 - I m 2 = 0

I m 1 = I m 2

Onde: I v = A . v

Resposta

a) v 2 = 12 m/s b) P 2 = 1,325.10 2 k P a c) I m 1 = I m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fonte projetada para pulverizar uma coluna de água com 12m de ar possui um bico de 1,0 cm de diâmetro ao nível do solo. A água desta bomba está a 3,0 m abaixo do solo. O tubo para o bico tem um di
Na Figura 13-39, H é a profundidade do líquido e h é a distância da superfície do líquido ao tubo inserido no lado do tanque. (a) Encontre a distância x em que a água atinge o chão depois de sair do t
Derive a equação de Bernoulli da maneira com mais generalidade do que é feito no texto, ou seja, permita que o fluido mude de altitude durante seu movimento. Usando o teorema de trabalho-energia, most
Um barril grande de altura H e área de seção transversal A 1 é preenchido com cerveja de raiz. O topo está aberto à atmosfera. Há uma abertura de torneira da área A 2 que é muito menor do que A 1 na p
No Exemplo 13-11, o fluido é acelerado ao entrar em uma parte estreita do tubo. Identifique as forças que atuam sobre o fluido na entrada da região estreita, responsáveis pela aceleração.