Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 87

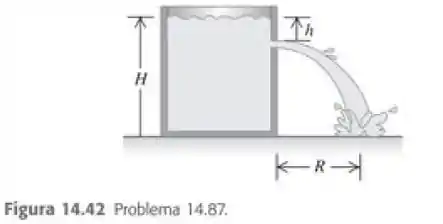
A água de um grande tanque aberto com paredes verticais possui uma profundidade H (Figura 14.42). Um orifício é aberto na parede vertical a uma profundidade j abaixo da superfície da água. a) Qual é a distancia R entre a base do tanque e o ponto onde a corrente atinge o solo? b) A qual distancia acima da base do tanque devemos dazer um segundo furo para que a corrente que emerge dele tenha um alcance igual ao do primeiro furo?

Passo 1

Depois de sair do tanque, a água cai em queda livre, com a x = 0 e a y = + g .

Do Exemplo 14.8, a velocidade do efluxo é 2 g h

Passo 2

  1. O tempo necessário para que qualquer parte da água alcance o solo é

    2. t = 2 ( H - h ) g

    em que momento a água viaja uma distância horizontal

    R = v t = 2 h ( H - h )

    Passo 3

  2. Note que se

h ' = H - h

h ' H - h ' = H - h h

E então

h ' = H - h

dá o mesmo intervalo. Um orifício H   -   h abaixo da superfície da água está a uma distância h   acima do fundo do tanque.

Para o caso especial de h   =   H   /   2 , h   =   h   ' e os dois pontos coincidem. Para o orifício superior, a velocidade do efluxo é menor, mas o tempo no ar durante a queda livre é maior.

Resposta

  1. 2 h H - h
  2. h ' = H - h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando tossimos, o ar é expelido em alta velocidade pela traqueia e brônquios superiores e remove o excesso de muco que está prejudicando a respiração. Essa alta velocidade é produzida da seguinte for
Petróleo de densidade 0,85g / c m 3 e viscosidade 1 poise é injetado, à pressão de 5a t m , numa extremidade de um oleoduto de 20c m de diâmetro e 50k m de comprimento, emergindo na outra extremidade
Para o escoamento com circulação constante definido pela: v = C Γ 2 π r , v → = vθ ^ , Demonstre que, num plano horizontal, a pressão p varia com a distância r ao eixo com uma taxa de variação dada po
Uma diferença de pressão de 6,00 X 10 4 Pa é necessária para manter uma vazão volumétrica de 0,800 m 3 / s para um fluido viscoso escoando por uma seção de tubo cilíndrico com raio de 0,210 m. Que dif
Uma vieira consegue locomover-se rapidamente na água (Figura P.8) abrindo (devagar) e fechando (depressa) sua dupla concha, como se fosse uma dobradiça, para produzir um jato de água e aproveitar o re