Quando tossimos, o ar é expelido em alta velocidade pela traqueia e brônquios superiores e remove o excesso de muco que está prejudicando a respiração. Essa alta velocidade é produzida da seguinte forma: depois que inspiramos uma grande quantidade de ar, a glote (abertura estreita da laringe) se fecha, os pulmões se contraem, aumentando a pressão do ar, a traqueia e os brônquios superiores se estreitam e a glote se abre bruscamente, deixando escapar o ar. Suponha que, durante a expulsão, a vazão seja . Que múltiplo da velocidade do som () é a velocidade do ar na traqueia se o diâmetro da traqueia (a) permanece com o valor normal de e (b) diminui para ?
Passo 1
Vamos tentar entender a situação como um problema de física. Dá uma olhada nesse diagrama bem simplificado de uma pessoa em perfil: (bem simplificado mesmo)
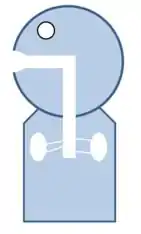
Beleza, aquelas duas bolotas no tronco do indivíduo são os pulmões. O ar é expelido dali, passa pelos brônquios (as linhas mais finas) até chegar na traqueia (o retângulo branco).
Independente da qualidade do desenho, o importante é você entender que a vazão ( em todos esses trechos é a mesma, ou seja, esse produto aqui é constante:
Onde é a área da seção reta do trecho, e é a velocidade do fluido (nesse caso o ar) naquele trecho.
O enunciado já diz que vale , e quer saber qual vai ser a velocidade do ar na traqueia dependendo da área dela.
Passo 2
Na letra (a), o diâmetro da traqueia é , ou . Se a gente aproximar a traqueia como um cilindro, a área da seção reta dela vai ser um círculo, então:
Pronto, agora podemos substituir isso na fórmula da vazão:
E como “múltiplo da velocidade do som” (como o enunciado pediu):
Pronto, agora é só fazer a mesma coisa na letra (b).
Passo 3
Dessa vez o diâmetro da traqueia vai ser . Vamos jogar isso na fórmula da área do círculo mais uma vez:
E agora substituindo isso na fórmula da vazão:
Agora pra achar a resposta em “múltiplos da velocidade do som”:
E essa é a resposta da letra (b)
Resposta
(a)
(b)