Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 88

Um balde cilíndrico, aberto na parte superior, possui diâmetro de 10,0 cm e altura igual a 25,0 cm. Um orifício circular com área da seção reta igual a 1,50 c m 2 é feito no centro da base do balde. A água flui para dentro do balde por um tubo acima dele com uma taxa igual a 2,40 × 10 - 4   m 3 / s . Até que altura a água subirá no balde?

Passo 1

Vamos usar a equação de Bernoulli para encontrar a velocidade com a qual a água flui pelo buraco.

O nível da água na embarcação aumentará até a taxa de fluxo de volume na embarcação, 2,40 × 10 - 4   m 3 / s , é igual à vazão do volume do orifício na parte inferior.

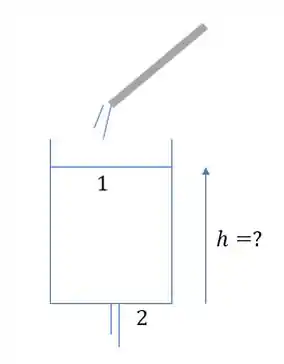
Os pontos 1 e 2 são escolhidos na figura acima.

Passo 2

A equação de Bernoulli:

p 1 + ρ g y 1 + 1 2 ρ v 1 2 = p 2 + ρ g y 2 + 1 2 ρ v 2 2

A vazão volumétrica fora do furo é igual à vazão volumétrica do tubo,

v 2 A 2 = 2,40 × 10 - 4   m 3 / s

Isso implica qie

v 2 = 2,40 × 10 - 4   m 3 / s 1,50 × 10 - 4 m 2 = 1,60   m / s

Passo 3

Como

A 1 ≫ A 2

E

v 1 A 1 = v 2 A 2

Isso nos diz que

1 2 ρ v 1 2 ≪ 1 2 ρ 2 2 ;

Negligenciando o termo

1 2 ρ v 1 2 .

Passo 4

p 1 = p 2 = p a   ( p r e s s ã o   d o   a r )

Então

p a + ρ g h = p a + 1 2 ρ v 2 2

E

h = v 2 2 2 g = 1,60 m s 2 / 2 9,80 m s 2 = 0,131   m = 13,1   c m

Quanto maior a vazão no balde, v 2 maiores estarão em equilíbrio e quanto maior a água vai subir no balde.

Resposta

13,1   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A água flui por um tubo horizontal com velocidade de fluxo igual à v 1 = 3,00 m/s e sob uma pressão P 1 = 200 kPa. Em determinado momento, o diâmetro do tubo pelo qual a água escoa é reduzido pela met
Considera-se uma tubulação horizontal flexível para transportar água (ilustrada acima).É necessária uma vazão mínima I v = 0,050 L / s . O tubo tem uma secção transversal circular de raio r 2 = 0,5 c
A pressão em uma seção de um cano horizontal de 2,00 cm de diâmetro é de 142kPa. Água escoa através do cano a 2,80 L/s. Se a pressão em um certo ponto é reduzida a 101 kPa, devido a um estrangulamento
O gasoduto do Alaska tem uma vazão máxima de I v = 240.000 m 3 / d , sabendo que a maior parte do tubo tem raio r 60 = 60,0 c m , encontre a pressão P ' em um ponto de raio r 30 = 30,0 c m , considera
A figura abaixo mostra um tubo estático de Pitot, um dispositivo usado para medir a velocidade de um gás. O tubo interno fica de frente para o fluido recebido, enquanto o anel de orifícios no tubo ext