Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 15
Para o escoamento com circulação constante definido pela:
Demonstre que, num plano horizontal, a pressão varia com a distância ao eixo com uma taxa de variação dada por , onde é a denisdade do fluido. Interprete esse resultado. Obtenha como função de a partir desta equação e explique o resultado obtido.
Passo 1
A circulação é a integral de linha da velocidade do fluido ao longo de um percurso :
A relação que o enunciado deu nos diz que:
Isso indica que a velocidade do fluido é sempre constante e perpendicular a um círculo de raio partindo da origem. Pois nesse caso:
Passo 2
Em geral, temos a seguinte relação entre a pressão e a densidade de força :
Como a nossa pressão só varia radialmente (porque a velocidade só varia radialmente), podemos reescrever esse gradiente como:
Ou seja, para encontrar a relação que foi pedida no enunciado, temos que calcular a densidade de força em um ponto qualquer do fluido.
Passo 3
Para que o fluido seja mantido em uma trajetória circular, precisamos ter:
Para uma pequena porção de flui:
E podemos reescrever :
O termo do lado esquerdo é justamente a densidade de força :
Então:
Que é exatamente o que queríamos demonstrar. Esse resultado indica que a pressão varia cada vez menos conforme nos afastamos da origem, em qualquer direção.
Passo 4
Para encontrar em função em função de a partir desse resultado, vamos substituir com a fórmula que foi dada no enunciado:
Então:
Integrando os dois lados:
E a constante que “sobrou” da integral representa o valor da pressão quando :
E podemos reescrever isso com:
Podemos inventar alguns valores para as constantes e fazer um gráfico para explicar o que esse resultado representa:
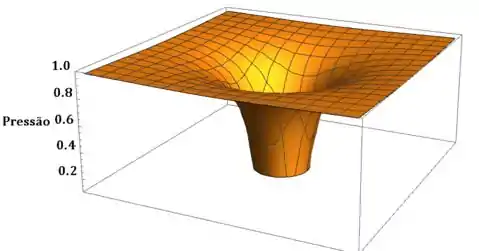
As unidades da pressão são arbitrárias, a ideia é só mostrar o seu comportamento.
Resposta
Ver demonstração. A pressão é dada por .