Uma alpinista com de peso é sustentada por uma corda de segurança presa a um grampo em uma das extremidades e a um mosquetão na cintura da moça na outra extremidade. A linha de açaí da força exercida pela corda passa pelo centro de massa da alpinista. Os ângulos indicados na figura são e . Se os pés da moça estão na iminência de escorregar na parede vertica, qual é o coeficiente de atrito estático entre os sapatos de alpinismo e a parede?

Passo 1
Falaa galerinha bonita, show de bolinhas?
Primeira coisa que devemos fazer é investigar as forças que atuam sobre a alpinista, de modo que teremos um digrama mais ou menos assim:
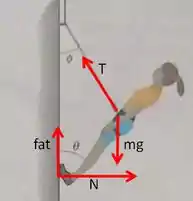
Onde é a força peso da alpinista que o enunciado nos deu como , é a tensão na corda a força normal atuando sobre o pé da alpinista e é a força de atrito que atua na parede.
Passo 2
Agora, vamos aplicar as equações do equilíbrio de forças e de torques:
Na vertical, temos:
Na horizontal:
A questão nos pede o valor de . Bora lá ver como que fica essa brincadeira então.
Substituindo o valor de encontrado na segunda equação na primeira, temos:
Passo 3
Agora a malandragem pra gente encontrar os valores de e está no equilíbrio de torques! Vamos investigar a equação desse equilíbrio com relação ao ponto de contato dos pés com a parede, considerando como e os comprimentos representados na figura:
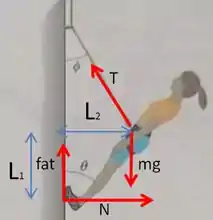
Então o somatório dos torques em relação ao ponto de contato dos pés, será dado como:
E como a gente é sagacidade pura, podemos ver que e estão relacionados através do triângulo retângulo que eles formam com a perna da alpinista, tal que:
Substituindo na equação anterior, vem:
“cortando” da jogada, temos:
Iradoso, agora se a gente isolar , vamos obter:
Passo 4
Maravilha, agora a gente só precisa substituir o valor de que a gente acabou de encontrar na equação para o coeficiente de atritio , logo:
Fazendo isso, temos: