Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.Problemas Adicionais - Ex. 83
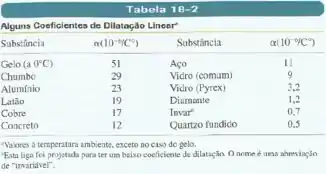
A temperatura de um disco de Pyrex varia de para . O raio inicial do disco é e a espessura inicial é . Tome esses dados como sendo exatos. Qual é a variação do volume do disco? (Veja a tabela .)
Passo 1
O que vai acontecer aqui é o seguinte: o vidro vai dilatar certo? Mas como estamos pensando tanto no raio quanto na espessura, vamos considerar as dilatações dos dois.
O coeficiente de dilatação linear é:
E a fórmula da dilatação é quase a mesma no raio e na espessura .
Ok, nosso objetivo é calcular a variação do volume quando a temperatura vai de para , ou seja:
Passo 2
Vamos encontrar uma fórmula para a variação do volume. Já que o disco tem espessura, vamos pensar nele como um cilindro:
A base é um círculo, e a altura é a espessura , então vamos colocar a fórmula que conhecemos:
E vamos dizer que, depois da dilatação, os raios passam a ser:
Substituindo isso na fórmula para o novo volume :
Agora vamos fazer um “truque” muito comum em questões de dilatação. Como as variações e costumam ser muito pequenas, nós vamos desconsiderar todos os termos em que essas variações aparecem ao quadrado, ou multiplicadas entre si.
Um número muito pequeno ao quadrado é um número extremamente pequeno! Então vãos descartar todos desse tipo:
Agora sim, vamos subtrair esse volume do volume inicial :
Passo 3
Beleza, agora vamos jogar as fórmulas da dilatação (que achamos no passo ) nessa variação de volume:
Ótimo, agora é só substituir os valores (lembre de converter os centímetros para metros):
Ou, em centímetros cúbicos:
Pronto, resolvido!
Resposta
A variação do volume é de .