Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 55
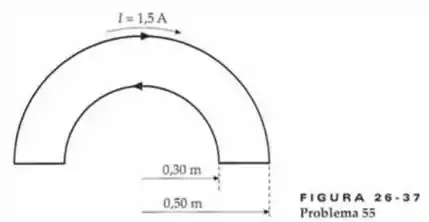
Um anel consiste em dois semicírculos conectados por segmentos retilíneos (Figura 26-37). Os raios interno e externo são e , respectivamente. Uma corrente de percorre este fio e, no semicírculo externo, ela está no sentido horário. Qual é o momento magnético deste anel de corrente?
Passo 1
O momento magnético é dado por
Para achar a área temos que considerar metade de uma coroa circular com raio interno e raio externo :
Como queremos metade da coroa:
Passo 2
Portanto, o momento magnético é dado por
Substituindo os valores
Logo,
Resposta
Exercícios de Livros Relacionados
A intensidade do pólo q m de um ímã em barra é definida como μ → = q m ⋅ l → , onde μ → é o momento magnético do ímã e l → é a posição do pólo norte do imã em relação ao pólo sul. Mostre que o torque
Um disco uniforme, fino, uniformemente carregado, de massa m , raio r e densidade superficial uniforme de carga σ , gira com rapidez angular ω em torno de um eixo que passa pelo seu centro e é perpend
Um disco fino não-condutor e não-uniforme tem massa m , raio R e carga total Q , com carga por unidade de área σ variando de acordo com σ 0 r / R , e massa por unidade de área de σ m que é dada por m
Uma espira circular de área A está contida no plano xy. Vista ao longo do eixo Oz, olhando para a origem no sentido z, uma corrente I circula no sentido horário em torno da espira. O torque produzido
Qual dos seguintes elementos é um candidato para a RM? (a) 12C6; (b) 16O8; (c) 40Ca20; (d) 31P15