Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 69

Um anel uniforme de 1,5 m de diâmetro pivota em torno de um ponto de seu perímetro, livre para girar em torno de um eixo horizontal perpendicular ao seu plano. O anel é largado com seu centro à mesma altura do eixo. (a) Se o anel é largado do repouso, qual é sua rapidez angular máxima? (b) Qual é a menor rapidez angular que lhe deve ser dada na largada para que ele gire uma volta completa?

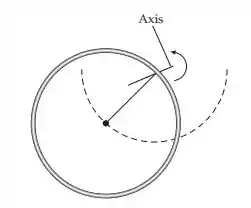
Passo 1

  1. Da conservação de energia vamos relacionar a energia potencial inicial com a energia cinética de rotação para o momento em que o centro de massa está diretamente abaixo do ponto de suporte.

    2. Δ K = m g Δ h

    1 2 I p ω m á x 2 = m g Δ h

    O teorema dos eixos paralelos (famoso teorema de Steiner) vai relacionar o momento de inércia com relação a um ponto com o momento de inércia com relação ao centro de massa.

    I p = I c m + m R 2 = m R 2 + m R 2 = 2 m R 2

    Logo,

    1 2 2 m R 2 ω m á x 2 = m g R

    ω m á x = g R = 9.81 0.75

    ω m á x = 3.6 r a d s

    Passo 2

  2. Também por conservação de energia, vamos ter que dar uma energia de rotação para o anel, que faça ele ser capaz de passar pelo ponto mais alto. Se passar por ele, o anel é capaz de dar a volta completa.

I ω 0 2 2 + m g R = m g 2 R

ω 0 2 = 2 m g R I

O momento de inércia é o mesmo da letra (a), ou seja, I = m R 2 + m R 2 = 2 m R 2 .

ω 0 2 = 2 m g R 2 m R 2 = g R

ω 0 = g R = 9.81 0.75

ω 0 = 3.6 r a d s

Resposta

  1. ω m á x = 3.6 r a d s
  2. ω 0 = 3.6 r a d s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma lata de metal contendo sopa condensada de cogumelo tem massa 215g , altura 10,8c m e diâmetro 6,38c m . Ela é colocada em repouso de lado no topo de uma rampa de 3,00m de comprimento que está a 25
Se a polia mostrada na Figura P10.71 tem raio R e momento de inércia I . Uma ponta do bloco de massa m é conectada a uma mola de constante força k , e a outra é presa a uma corda ao redor do carretel.
Uma bola de tênis é uma esfera oca com parede fina, posta para rolar sem escorregar a 4,03m / s na seção horizontal da pista, como mostrado na Figura P10.62. Ela rola em torno da parte interna de um l
Considere dois corpos com m 1m 2 conectados por uma corda leve que passa sobre uma polia tendo um momento de inércia de I em torno de seu eixo de rotação conforme mostrado na Figura P10.44. A corda nã
Princípios Da Física – Serway – Vol.1 – 5ª Ed., Cap.10, Problemas, Questão 40Na Figura P10.40, o corpo pendurado tem massa de m 1=0,420k g ; o bloco deslizante tem massa de m 2=0,850k g ; e a roldana