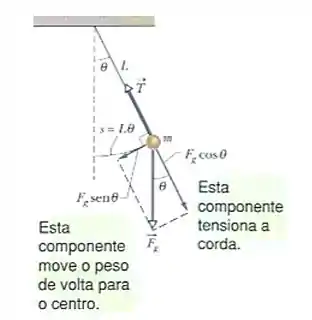
O ângulo do pêndulo da Fig. 15-9b é dado por . Se, em , e , qual é (a) a constante de fase e (b) o ângulo máximo ? (Sugestão: não confunda a taxa de variação de , , com a frequência angular do MHS.)

Bom, pra achar o valor da constante de fase, vamos dividir a equação da posição pela equação da velocidade. Fazendo isso, a gente consegue achar uma expressão direta para descobrir avaliado em .

onde é a frequência angular de oscilação do sistema. O valor de em é e o valor de é , então nós podemos encontrar a fase