Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 24
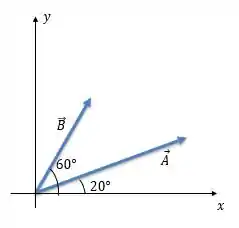
A FIGURA P3.24 mostra os vetores e . Seja .
- Reproduza a figura sobre sua folha de papel tão precisamente quanto possível, usando uma régua e um transferidor. Sobre sua figura, desenhe o vetor usando o método gráfico de soma de e . Depois, determine o módulo e a orientação de medindo-os com a régua e o transferidor.
- Com base na figura do item anterior, usando geometria e trigonometria, calcule o módulo e determine a orientação de .
- Decomponha os vetores e , depois use os componentes para determinar algebricamente o módulo e a orientação de .
Passo 1
- Reproduza a figura sobre sua folha de papel tão precisamente quanto possível, usando uma régua e um transferidor. Sobre sua figura, desenhe o vetor usando o método gráfico de soma de e . Depois, determine o módulo e a orientação de medindo-os com a régua e o transferidor.
- Com base na figura do item anterior, usando geometria e trigonometria, calcule o módulo e determine a orientação de .
Para realizar a soma gráfica vamos refazer a figura, mas colocando a calda do vetor na ponta do vetor :
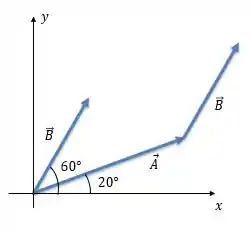
Agora vamos ligar a caldo do vetor com a ponta do vetor e teremos o vetor :
Prontinho!
Quando a gente mede com a régua e transferidor vamos achar que:
Passo 2
Dá uma olhada nessa imagem aqui:
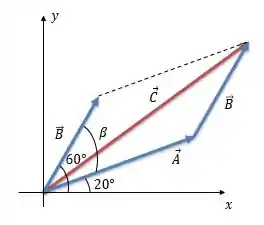
Vamos utilizar a lei dos cossenos para calcular o módulo:
Os módulos dos vetores e foram dados na figura:
E
Então:
Logo:
Passo 2
Para acharmos o ângulo vamos utilizar a lei dos senos.
Vou redesenhar aqui a imagem pra ficar mais claro:
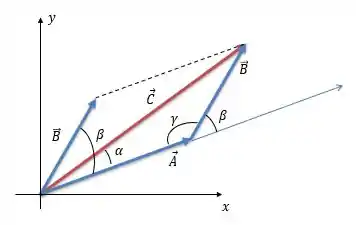
Olhando para o triângulo formado pelos vetores , e , podemos escrever a lei dos senos:
Precisamos saber quem é e pela imagem vemos que:
E:
Retornando a lei dos senos:
Para acharmos quem é temos que fazer a função inversa do seno, o arcseno:
Mas não é que queremos saber né, é :
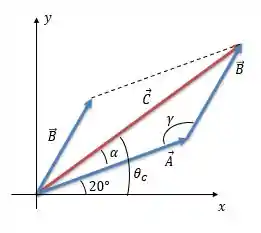
Passo 3
- Decomponha os vetores e , depois use os componentes para determinar algebricamente o módulo e a orientação de .
Vamos decompor os vetores e , sempre lembrando daquele macete: A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
Para :
Temos que:
Então:
Para :
Temos que:
Então:
Passo 4
Agora que já achamos as componentes de e , vamos achar as componentes do vetor .
Como é a soma entre os vetores e , as componentes de também serão a soma das componentes de e :
Passo 5
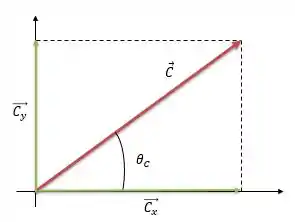
Agora para calcular o módulo vamos fazer:
Agora, para achar o ângulo vamos fazer:
Ufa!! Demorou, mas foi =)
Resposta
- ;
- ;
- ;