Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 8
Seja:
, e
.
Determine o módulo e o componente de cada vetor.
Passo 1
Já que a questão pede para acharmos a componente , antes de começarmos a fazer a questão, vamos lembrar como decompor e achar os valores das componentes de um vetor, beleza?
Nós iremos decompor um vetor em duas componentes, uma na direção do eixo e outra na direção do eixo como na Figura:
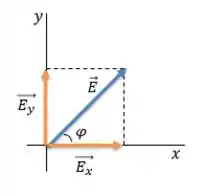
E o valor de cada componente, em função do ângulo fica assim:
A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
Pegou o macete?
Então agora bora lá resolver a questão! Vem comigo.
Passo 2
Vamos começar pelo vetor .
Vamos desenhar esse vetor e as componentes, porque assim fica mais fácil, okay?
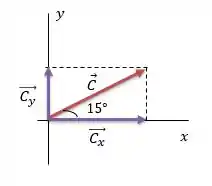
Na figura temos o vetor , ele está acima do semi-eixo positivo e o ângulo que ele forma com esse eixo é igual a .
Agora vamos achar o valor da componente desse vetor. Não esquece o macete ein:
Para acharmos o valor de , precisamos saber quem é o módulo, , do vetor.
A questão pede pra encontrar esse módulo também, mas não precisa encontrar em desespero okay? Porque a questão já nos fornece o módulo
Quando a questão diz que o vetor , ela está nos dizendo que o módulo do vetor é igual a e a informação seguinte nos diz a direção e sentido do vetor, show de bola?
Então, temos que:
E temos também que:
Então:
Passo 3
Agora vamos para o vetor .
Vamos desenhar também esse vetor:
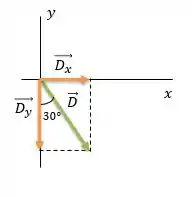
Na figura temos o vetor , ele está à direita do semi-eixo negativo e o ângulo que ele forma com esse eixo é igual a .
Agora vamos achar o valor da componente desse vetor. Não esquece o macete ein:
O módulo, , do vetor a questão nos fornece, daquele mesmo jeitinho que fornece para o vetor . Então, temos que:
E sabemos que:
Logo:
Resposta
;
;