Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 25
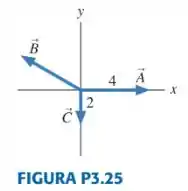
Para os três vetores mostrados na FIGURA P3.25, .Qual é o vetor ?
- Expresse em termos de componentes.
- Expresse em módulo e orientação.
Passo 1
- Expresse em termos de componentes.
- Expresse em módulo e orientação.
Podemos escrever um vetor em termos dos vetores unitários dessa maneira:
Vamos olhar para o vetor :
Ele está na direção do eixo , apontando para o sentido positivo desse eixo, então ele não tem componente :
Agora o vetor :
Ele está na direção do eixo , apontando para o sentido negativo desse eixo, então ele não tem componente :
Já conhecemos quem são os vetores e , para acharmos , vamos utilizar o vetor soma que a questão nos forneceu:
Passo 2
Para calcula o módulo vamos fazer:
As componentes desse vetor nós calculamos na letra a:
Então, o módulo será:
Passo 2
Agora, para acharmos a orientação precisamos achar o valor do ângulo que o vetor faz com o semi-eixo negativo:
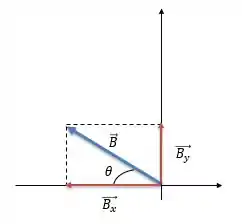
Para achar esse ângulo vamos fazer o seguinte:
O vetor tem módulo igual a e está a acima do semi-eixo negativo.
Resposta
- O vetor tem módulo igual a e está a acima do semi-eixo negativo.