Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Problemas - Ex. 67
a)Pela expressão de E ( e ), encontre a expressão do potencial elétrico V em função de r, para todos os pontos no interior e no exterior do cilindro. Seja V=0 na superfície do cilindro. Em cada caso, expresse os resultados em função da carga por unidade de comprimento da distribuição de cargas.
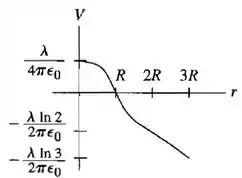
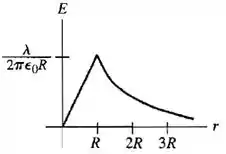
b)Faça um gráfico de V e E em função da distância e de r=0 até r=3R.
Passo 1
letra a)
Podemos achar a diferença de potencial através da expressão:
E a expressão do campo elétrico ele nos deu no enunciado.
Passo 2
Para pontos fora do cilindro temos . Então
Escrevemos então:
Na superfície do cilindro o potencial é zero ()
Passo 3
Para pontos dentro do cilindro temos . Então
Logo:
Como antes
Passo 4
letra b)
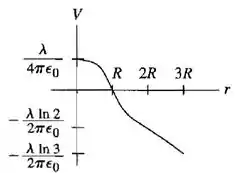
O potencial dentro do cilindro é positivo e decrescente. Quando chega na superfície ele é zero e fora do cilindro ele decresce e é negativo
Passo 5
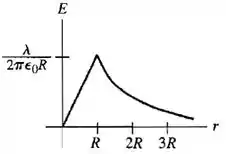
Já o campo elétrico dentro do cilindro ele é crescente e positivo. E fora do cilindro ele cai na razão de 1/r.
Resposta
letra a),
letra b)
