Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 89

Três finas cascas esféricas condutoras e concêntricas têm raio a , b e c e a < b < c . Inicialmente, a casca interna está descarregada, a casca intermediária tem uma carga positiva + Q e a casca externa tem uma carga - Q . (Considere que o potencial seja zero em pontos bem distantes das cascas.) (a) Determine o potencial elétrico de cada uma das três cascas. (b) Se as cascas interna e externa forem agora, conectadas por um fio condutor que está isolado e que passa através de um pequeno orifício pela esfera intermediária, qual é o potencial elétrico de cada uma das três cascas e qual é a carga final em cada uma?

Passo 1

Fala galera, beleza? Lembre-se que o potencial elétrico no interior de uma casca esférica de raio R é

V = k Q R

onde Q é a carga da casca. Já o potencial para pontos externos é

V = k Q r

onde r é a distância do ponto até o centro ( r > R ).

  1. Temos o seguinte esquema:

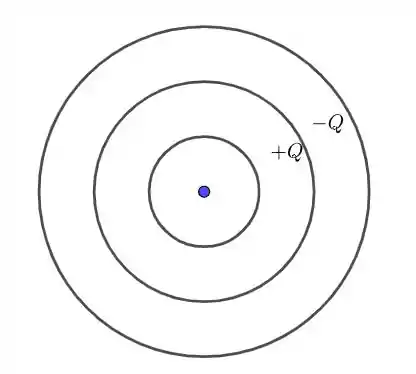
    2. Vamos calcular o potencial de cada casca:

  • Casca interna:

    • V 1 = k + Q b + k - Q c = k Q 1 b - 1 c

  • Casca intermediária:

    • V 2 = k + Q b + k - Q c = k Q 1 b - 1 c

    Note que V 1 = V 2 ! Isso é esperado, pois a casca interna não está carregada.

  • Casca externa

V 3 = k + Q c + k - Q c = 0

Passo 2

  • Se conectarmos as esferas com um fio, o potencial delas será o mesmo, ou seja,

    • V 1 = V 3

    Agora, a carga da casca interna será Q 1 e da casca externa Q 3 . Logicamente, devemos ter

    Q 1 + Q 3 = - Q

    Note que o potencial da casca externa agora será dado por:

    V 3 = k Q 1 c + k + Q c + k Q 2 c = 0

    Assim, V 1 = V 2 = 0 . Assim,

    V 1 = k Q 1 a + k + Q b + k Q 3 c = 0 Q 1 a + Q b + Q 3 c = 0 ⟹ Q 1 a + - Q - Q 1 c = - Q b Q 1 1 a - 1 c = Q - 1 b + 1 c ⟹ Q 1 c - a a c = - Q c - b b c Q 1 = - Q ⋅ a c - b b c - a

    Dessa forma,

    Q 3 = - Q - Q 1 = - Q c b - a b c - a

    Por fim, temos

    V 2 = k Q 1 b + k + Q b + k Q 3 c Utilizando os resultados de Q 1 e Q 3 , e simplificando obtemos

    V 2 = k Q ⋅ c - b b - a b 2 c - a

    É isso ai, galera! :D

    Resposta

    Ei, a resposta está no passo a passo :)

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    No modelo de Bohr para o átomo de hidrogênio (Cap.2, Probl.3), calcule:A razão da energia potencial eletrostática do elétron a sua energia cinética;A energia necessária para ionizar o átomo, em elétro
    Em suas célebres experiências de 1906 que levaram à descoberta do núcleo atômico, Rutherford bombardeou uma fina folha de ouro (número atômico 79) com partículas α (núcleos de He, de carga 2 e ), prod
    Uma casca hemisférica de raio R está uniformemente carregada com carga positiva de densidade superficial σ .Ache o potencial V ( O ) no ponto central O . (Tomando V ∞ = 0 )Uma partícula de massa m e c
    Usando a expressão do campo elétrico, E = Q 4 π ϵ o r 2 p a r aR ≤ r ≤ 2 R , calcule a diferença de potencial entre a esfera condutora maciça e a fina casca isolante.
    Uma casca esférica isolante, com raio interno de 25c m e raio externo de 60c m , possui uma carga de + 150μ C uniformemente distribuída pela sua superfície. O ponto a está no centro da casca, o pontob