Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 134
APLICAÇÃO BIOLOGICA. Depois que um paraquedista salta de um avião (mas antes de puxar o cordão que faz abrir o paraquedas), uma rapidez para baixo de pode ser atingida. Quando finalmente o paraquedas é aberto, a força de arraste aumenta de cerca de um fator de dez e isto pode provocar um grande baque sobre o saltador. Seja um paraquedista caindo a antes de abrir o paraquedas. (a) Supondo que a massa do paraquedista é de , determine sua aceleração no momento em que o paraquedas acaba de ser aberto. (b) Se rápidas variações de aceleração maiores que podem causar danos à estrutura do corpo humano, esta prática é segura?
Passo 1
Item a) Olá, querido! Temos dois momentos aqui. Primeiro, o paraquedista pulou do avião e atingiu uma velocidade de .
A gente pode considerar que ele atinge essa velocidade e permanece nela, assim sua aceleração fica em . E aí nessa situação a gente tem a chamada rapidez terminal, que acontece quando a força de arraste (para cima) se iguala a força gravitacional (para baixo).
Podemos lembrar também que a força de arraste para uma rapidez grande como a nossa pode ser expressa como proporcional ao quadrado da velocidade no momento, assim:
Onde é uma constante de proporcionalidade. Nessa situação, a gente pode fazer o diagrama de corpo livre do nosso paraquedista:
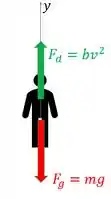
Só que ele abre o paraquedas. Isso faz com que aumente de um fator de . Aí a aceleração dele deixa de ser nula porque há uma força maior sobre ele voltada para cima. E a pergunta do nosso enunciado é essa: qual é a aceleração dele quando abre o paraquedas?
Passo 2
Cara, vamos começar montando a segunda lei de Newton para esse primeiro momento, para ter uma equaçãozinha que vai ajudar a gente no futuro. Temos
Só que como ele está na rapidez terminal, temos . E lembrando que e :
Passo 3
Agora vamos olhar o segundo momento onde tem a aceleração que a gente quer achar. Vamos fazer o diagrama de corpo livre:
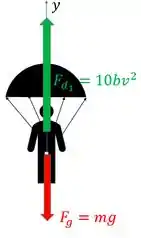
Lembra que depois que ele abriu o paraquedas, ficamos com 10 vezes mais força de arraste, por isso agora . A segunda lei de Newton fica:
Passo 4
Percebe que a única informação que a gente não tem em , além da aceleração , é o valor de . Mas a gente pode achar esse cara pela equação do passo 2:
Substituindo isso na equação do passo anterior:
Simplificando:
Sabendo que
Passo 5
Item (b)
Ele diz que variações maiores que (5 vezes a aceleração da gravidade) são prejudiciais à saúde e pergunta se a variação que nosso paraquedista sofre torna a prática desse esporte segura.
A gente viu que ele saiu de para . Ou seja, tivemos uma variação de aceleração de .
Como essa variação de aceleração excede a aceleração segura em , ela não é uma prática segura.
Resposta
(b) Essa prática não é segura.