Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 25
Um skydiver (paraquedista) de pode ser modelado como uma “caixa” retangular com dimensões . Qual é sua velocidade terminal se ele cai em pé?
Passo 1
Vamos representar o paraquedista como um caixa retangular, em pé, porque o paraquedista cai em pé, e desenhar as forças que atuam sobre ele:
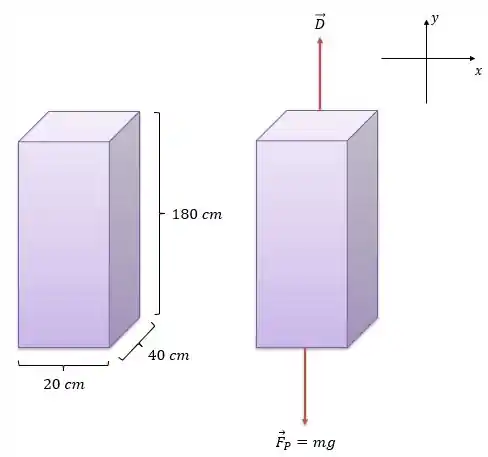
As foças que atuam sobre o paraquedista são: a força peso e a força de arraste. A força peso aponta para baixo, no sentido negativo de . O paraquedista cai em direção a superfície da terra, ou seja, o movimento é vertical, no sentido do eixo negativo e por isso a força de arraste, , aponta no sentido do eixo positivo porque ela tem o sentido oposto ao do movimento.
Passo 2
O que queremos saber é a velocidade terminal do paraquedista, então precisamos lembrar que:
A VELOCIDADE TERMINAL CORRESPONDE A SITUAÇÃO EM QUE A FORÇA RESULTANTE QUE ATUA NO CORPO SE TORNA ZERO.
Então, quando a velocidade for a velocidade terminal, , teremos que:
Passo 3
Lembra da fórmula da força de arraste?
é a velocidade em que o objeto se movimenta e o é a área transversal sobe a qual a força de arraste atua.
Como o paraquedista cai em pé, temos que:
Para que a força de arraste seja dada em Newton é preciso que essa área esteja em , então vamos converter:
Então:
Passo 4
Vimos que quando a velocidade terminal é atingida a força de arraste se iguala a força peso:
Vamos substituir o valor que encontramos para :
No lugar da velocidade coloquei a velocidade terminal, porque essa igualdade é verdadeira quando a velocidade é a velocidade terminal, show de bola?
Podemos isolar a :
A massa a questão forneceu e a aceleração da gravidade é um valor fixo:
Logo: