Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 133
Sueli alega que esquilos voadores na verdade não voam; eles saltam e usam as dobras da pele que liga as pernas dianteiras às traseiras como um paraquedas para planarem de árvore em árvore. Luísa decide testar a hipótese de Sueli, calculando a rapidez terminal de um esquilo voador em posição de voo. Se a constante da força de arraste é proporcional à área que o Objeto expõe ao fluxo de ar, use o coeficiente de um humano como sendo e algumas suposições sobre o tamanho de um esquilo para estimar sua rapidez terminal (para baixo). A alegação de Sueli é confirmada pelos cálculos de Luísa?
Passo 1
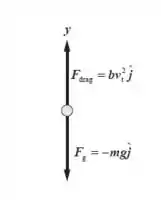
O diagrama do corpo livre que está abaixo mostra as forças que agem sobre o esquilo com velocidade terminal. Vamos supor que é proporcional a área frontal do esquilo e que esta área é cerca de vezes a de um ser humano. Além disso, vamos supor que a massa de um esquilo é de cerca de .
Aplicando a segunda lei de Newton nos leva a uma expressão para a velocidade do terminal do esquilo.
No exemplo 5-8 que ele fala
Passo 2
Aplicando a 2° Lei de Newton no eixo y:
Considerando em velocidade terminal, então :
Substituindo e :
Passo 3
Assumindo que a área , como o é proporcional a área frontal, então:
Substituindo por valores numéricos na expressão da velocidade terminal:
Porque a velocidade terminal do esquilo é de aproximadamente 80 km / h e esse valor é menos da metade da velocidade terminal de um humano, a afirmação de Sueli é confirmada pelo cálculo de Luiza.
Resposta
Ei, a resposta está no passo a passo :)