Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 44

APLICACAO EM ENGENHARIA O circuito mostrado na Figura 29-35 e chamado de filtro RC passa-altas porque ele transmite sinais de tensao de entrada que tenham altas frequencias com maior amplitude do que sinais de tensao de entrada que tenham baixas frequencias.Se a tensao de entradadada por V ent  = V emt pico  c o s ⁡ ( ω t ) ,mostre que a tensao de saida e V saita  = V H c o s ⁡ ( ω t - δ )  onde  V H = V cat  p l o o / 1 + ( ω R C ) - 2 . Considere que a saida esteja conectada a uma carga que conduz uma corrente insignificante.)Mostre que este resultado justifica o fato de este circuito ser chamado de filtro passa-altas.

Passo 1

E ai galera!! Vamos começar aqui essa questão?? Vai ser bem rápido e eu garanto que vocês vão entender!!

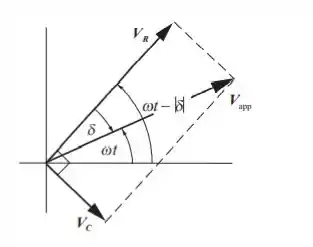
O diagrama fasorial para o filtro passa-alta RC é mostrado à direita. V → app  e   V → R   são os fasores de V i n e V o u t , respectivamente. Observe que t a n ⁡ δ = - X c / R . O δ ser negativo segue do fato de que V → app  está atrasado de V → R | δ | . A projeção de V → app  , no eixo horizontal é V a p p = V i n , e a projeção de V → R , no eixo horizontal é V R = V out  .

Passo 2

Expresse V a p p :

V app  = V app pico  c o s ⁡ ω t   o n d e   V app pico = V pico  = I pico  Z   e     Z 2 = R 2 + X C 2                     ( 1 )

Como δ < 0 :

ω t + | δ | = ω t - δ

V R é dado por:

V R = V R ,  pico  c o s ⁡ ( ω t - δ )   o n d e V R ,  pico  = V I I = I pico  R

Resolvendo a equação (1) para Z e substituindo X C , temos:

Z = R 2 + 1 ω C 2               ( 2 )

Passo 3

Como V o u t = V R :

V out  = V R ,  pico  c o s ⁡ ( ω t - δ ) = I in pico  R c o s ⁡ ( ω t - δ ) = V in pico  Z R c o s ⁡ ( ω t - δ )

Usando a equação (2) para substituir Z:

V out  = V in pico  R 2 + 1 ω C 2 R c o s ⁡ ( ω t - δ )

Simplifique ainda mais para obter:

V out  = V in pico  1 + ( ω R C ) - 2 cos ⁡ ω t - δ

Ou

V out  = V H cos ⁡ ω t - δ

Onde

V H = V in pico  1 + ( ω R C ) - 2

Como ω → ∞ ,

V I I → V in pico  1 + ( 0 ) 2 = V in pico 

mostrando que o resultado é consistente com o nome passa-alta para este circuito.

Resposta

Ver resolução

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bobina com 88 m H de indutância e resistência desconhecida e um capacitor de 0,94 μ F são ligados em série com um gerador cuja frequência é 930H z . Se a constante de fase entre a tensão aplicada
Uma fonte alternada de frequência variável, um capacitor de capacitância C e um resistor de resistência R são ligados em série. A Fig. mostra a impedância Z do circuito em função da frequência angular
(a) Em um circuito R L C , a amplitude da tensão entre os terminais do indutor pode ser maior que a força eletromotriz do gerador? (b) Considere um circuito R L C com E m = 10V , R = 10 Ω , L = 1,0 H
Em um circuito L C oscilante, quando uma energia igual a 75% da energia total está armazenada no campo magnético do indutor, determine (a) a fração da carga máxima que está armazenada no capacitor e (
Em um circuito L C oscilante, L = 25,0 m H e C = 7,80 μ F . No instante t = 0 , a corrente é 9,20m A , a carga do capacitor é 3,80 μ C e o capacitor está sendo carregado. Determine (a) a energia total