Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.3 - Ex. 25
Após emergências com grande perda de sangue, um paciente é colocado na posição de Trendelenburg, na qual o pé da cama é elevado para obter o máximo de fluxo sanguíneo para o cérebro. Se o coeficiente de atrito estático entre um paciente normal e os lençóis é , qual é o ângulo máximo no qual a cama pode ser inclinada com relação ao piso antes que o paciente comece a deslizar?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o ângulo máximo no qual a cama pode ser inclinada com relação ao piso antes que o paciente comece a deslizar, sabendo que o coeficiente de atrito estático é .
Considerando que no ângulo de inclinação máximo, o paciente está pronto para deslizar para baixo, então o atrito estático está em seu máximo e as forças no paciente estão em equilíbrio.
Seja descendo, temos no ângulo máximo a força de atrito estático:
Além disso, o somatório de forças horizontais deve ser zero, , para manter o paciente em equilíbrio. Então, vamos esboçar um diagrama de corpo livre do nosso sistema e analisar as forças atuando nele, considerando suas componentes horizontais e verticais e determinar o ângulo máximo .
Vamos lá!
Passo 2
O diagrama de corpo livre para o paciente é apresentado na figura:
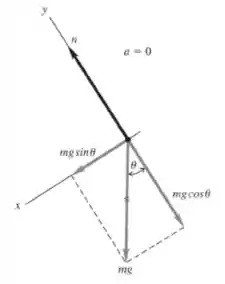
Somando as forças horizontais usando a segunda lei de Newton, temos:
Onde é a força de contato entre o paciente e a superfície.
Agora, considerando as forças horizontais, vamos ter:
Onde representa uma componente horizontal da força peso do paciente e representa a força de atrito. Mas nós vimos que , então substituindo, teremos:
Simplificando a equação, ficamos com:
E para , temos:
Um ângulo maior de inclinação faria com que mais sangue flua para o cérebro, mas também causaria o paciente deslizar para baixo da cama.
Valeu, galera! Até a próxima! 😉