Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 112
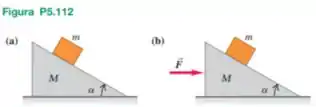
Uma cunha de massa repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa é colocado sobre a cunha (Figura P5.112a). Não existe nenhum atrito entre o bloco e cunha. O sistema é liberado a partir do repouso. (a) Ache a aceleração da cunha e os componentes horizontais e verticais da aceleração do bloco. (b) Suas respostas ao item (a) se reduzem ao valor esperado quando for muito grande? (c) Em relação a um observador estacionário, qual é a forma da trajetória do bloco?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a aceleração da cunha e os componentes horizontais e verticais da aceleração do bloco, analisar as respostas obtidas e determinar a forma da trajetória.
O primeiro passo nesse tipo de problema é desenhar as forças que agem em cada corpo:
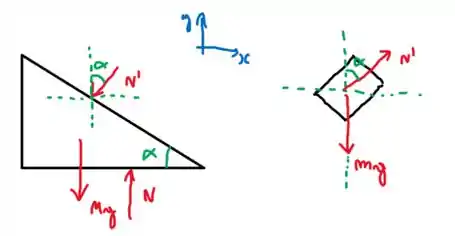
Repare que a cunha aplica uma normal sobre o bloco que, por sua vez, aplica uma força igual no sentido contrário sobre a cunha.
Nosso objetivo é achar as componentes da aceleração de cada corpo. Para a cunha, a força resultante na direção vertical deve ser nula:
Já na horizontal, temos que
Para o bloco, temos na vertical:
Na horizontal:
Vamos lá!
Passo 2
Com o que foi feito no passo , nós encontramos equações para incógnitas:
Precisamos de mais uma equação para resolver o problema. Para isso, vamos usar o fato que o bloco deve manter o contato com a cunha, de modo que que a aceleração resultante sobre ele deve ser paralela ao plano inclinado:
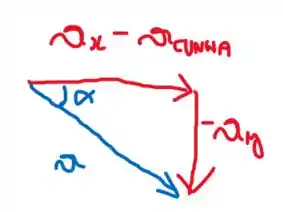
Detalhe que estou chamando o cateto de pois a orientação do sistema de coordenadas aponta para cima na direção vertical.
Portanto,
Substituindo isso no sistema, temos que
Isolando na última equação, temos que
Substituindo na segunda equação:
Simplificando todas as massas, podemos escrever
Abrindo a tangente, temos que
Fazendo o mmc, temos que
Passo 3
Observe que da primeira e terceira equação do sistema nós podemos tirar
Substituindo essa relação na equação do passo anterior:
Logo,
Ou ainda,
Com isso, achamos a aceleração da cunha:
Repare que essa aceleração é negativa, o que faz bastante sentido já que a cunha se movimenta para trás conforme o bloco desce.
Passo 4
Agora que temos a aceleração da cunha podemos achar a aceleração do bloco:
Portanto,
Para achar a componente da aceleração, usamos
Assim,
Com isso, achamos
Passo 5
Agora vamos para o item (b)! Queremos tomar o limite com , de modo que
Com isso, temos que
Observe que nesse caso nós retomamos os resultados do plano inclinado: a cunha em repouso e uma aceleração na direção do plano inclinado!
Passo 6
A trajetória será retilínea, já que a aceleração é constante ao longo do movimento.
Valeu, galera! Até a próxima! 😉