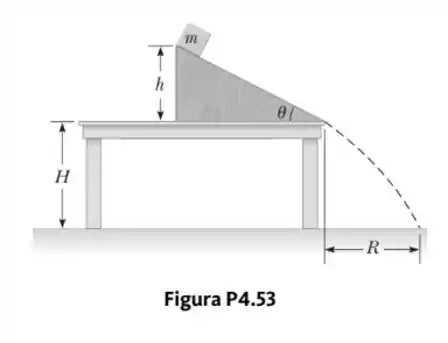
Um bloco de massa é liberado do repouso a acima da superfície de uma mesa, no topo de um plano inclinado com , conforme mostrado na Figura P4.53. O plano inclinado é fixado sobre uma mesa de altura .
- Determine a aceleração do bloco enquanto ele desce pelo plano inclinado.
- Qual é a velocidade do bloco quando ele sai da inclinação?
- A que distância da mesa o bloco atingirá o chão?
- Qual o intervalo de tempo decorrente entre o momento em que o bloco é liberado e o momento em que atinge o chão?
- A massa do bloco afeta algum dos cálculos acima?
Passo 1
E aiii galera, vamos fazer mais uma questão aqui?
Vem comigo!
Letra a:
Aplicando a segunda lei de Newton ao bloco quando ele está inclinado. Nós temos:
Abaixo, temos o esquema para facilitar:
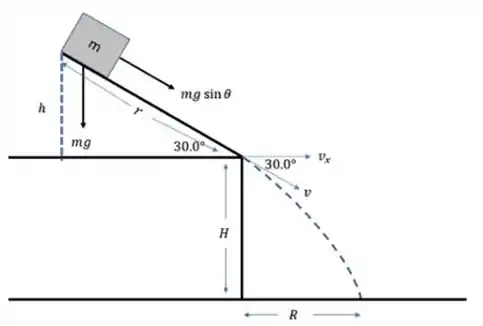
Passo 2
Letra b:
Agora, precisamos calcular o comprimento da inclinação, então, do triângulo da direita, obtemos:
Substituindo em uma equação cinemática adequada, obtemos a velocidade final do bloco quando sair da inclinação:
Então, o tempo é:
Passo 3
Letra c:
Quando o bloco sai da inclinação, cai como um projétil, e para obter seu alcance, nós precisamos primeiro obter o tempo que leva para chegar ao solo. Ao substituir os valores, temos uma equação cinemática adequada, nós temos:
Substituindo:
Passo 4
Letra d:
O tempo total é:
Passo 5
Letra e:
Podemos ver na primeira equação que a aceleração do bloco na inclinação depende apenas da aceleração gravitacional e do ângulo e enquanto há queda sua aceleração é a aceleração gravitacional.
Portanto, seu movimento não depende da massa, uma vez que a aceleração gravitacional é uma constante universal.
Resposta
- Portanto, seu movimento não depende da massa, uma vez que a aceleração gravitacional é uma constante universal.