Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 55
Uma artista amiga sua precisa de ajuda para pendurar uma escultura de 500 lb no teto. Por razões artísticas, ela deseja usar apenas duas cordas. Uma delas deverá formar 30° com a vertical, e a outra, 60°. Ela precisa que você determine o mínimo diâmetro da corda que poderá sustentar com segurança esta valiosa peça de arte. Depois de visitar lojas de ferragens, você descobre que as cordas são fabricadas com incrementos de 1/8 de polegada no diâmetro e que a carga segura recomendada é de 4.000 libras por polegada quadrada de secção transversal. Qual é o diâmetro da corda que você deve comprar?
Passo 1
Fala aí! Visualiza que nosso problema se parece com isso aqui:
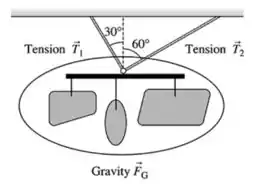
E a gente quer descobrir as tensões. Como são duas variáveis, vamos precisar de duas equações pra resolver… E a gente pode descobrir aplicando a segunda lei de newton separadamente nos componentes x e y. Olha:
Agora pra y:
Assim, a gente pode relacionar as duas tensões
Agora a gente pode substituir em uma das equações.
Agora, a gente pode descobrir T1 com a relação que a gente encontrou.
Pronto! Sabemos a tensão necessária pra cada uma das cordas. A gente precisa saber o diâmetro necessário correspondente.
Passo 2
O enunciado diz que o ideal é ser 4000 lbs por polegada quadrada, então a gente tem que verificar qual o diâmetro necessário pra atingir essa meta. Bora fazer a regra de três. Vamos considerar a tensão maior pra fazer as contas (melhor sobrar força do que faltar, certo?!)
A área da da secção transversal é dada por
E como queremos o diâmetro, vamos isolar o d.
Isso significa que nossa corda tem que ter um diâmetro mínimo de 0.371 polegadas. Porém, o cara da loja só vende diâmetros múltiplos de ⅛. Precisamos saber o mínimo suficiente.
Passo 3
Pra saber o diâmetro mínimo suficiente disponível na loja, vamos fazer outra regra de 3.
Isso significa que o diâmetro mínimo disponível pra gente comprar é o de ⅜.
Resposta
⅜ polegadas.